题目内容
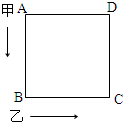 如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )
如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )| A、AB边上 | B、DA边上 | C、BC边上 | D、CD边上 |
分析:由题意可知,甲乙的速度差为72-65=7米/分钟.开始时两人距离差为90×3=270米,所以乙追上甲需要的时间为270÷7=38
分钟,此时甲行了65×38
=2507
米,长方形的周长为90×4=360米.2507
÷360=6
(周).
<
<1,所以当乙第一次追上甲时在正方形的DA边上.
| 4 |
| 7 |
| 4 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 81 |
| 84 |
| 3 |
| 4 |
| 81 |
| 84 |
解答:解:(90×3÷7)×65÷(90×4)
=
×65÷360,
=6
(周).
<
<1,
所以当乙第一次追上甲时在正方形的DA边上.
故选:B.
=
| 270 |
| 7 |
=6
| 81 |
| 84 |
| 3 |
| 4 |
| 81 |
| 84 |
所以当乙第一次追上甲时在正方形的DA边上.
故选:B.
点评:根据路程差÷速度差=追及时间求出乙追上甲时所用的时间是完成本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,ABCD是边长为10米的正方形,甲从A、乙从D同时开始按逆时针方向沿着正方形的边行走,甲的速度是乙速度的4倍,当甲、乙两人第一次距离(直线距离)最远时,甲行走的路程是
如图,ABCD是边长为10米的正方形,甲从A、乙从D同时开始按逆时针方向沿着正方形的边行走,甲的速度是乙速度的4倍,当甲、乙两人第一次距离(直线距离)最远时,甲行走的路程是