题目内容
数一数,下面各图中分别有几条射线,几个角,填在下表中.
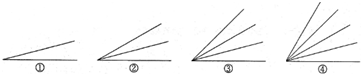
从上表中,你发现的规律是:

| 图号 | 1 | 2 | 3 | 4 |
| 射线条数 | 2 | |||
| 角的总个数 | 1 |
从一点引出n条射线,所组成的角的个数为:1+2+3+4+…+(n-1)=n(n-1)÷2
从一点引出n条射线,所组成的角的个数为:1+2+3+4+…+(n-1)=n(n-1)÷2
.分析:两条射线一个角,三条射线1+2=3个角,四条射线1+2+3=6个角,五条射线1+2+3+4个角,由此可以看出从一点引出n条射线,所组成的角的个数为:1+2+3+4+…+(n-1)=n(n-1)÷2.
解答:解:填表如下:
从上表中,你发现的规律是:从一点引出n条射线,所组成的角的个数为:1+2+3+4+…+(n-1)=n(n-1)÷2.
| 图号 | 1 | 2 | 3 | 4 |
| 射线条数 | 2 | 3 | 4 | 5 |
| 角的总个数 | 1 | 3 | 6 | 10 |
点评:解答此题注意数角的方法,先以第一条射线为一边,再以第二条射线为一边,以此类推,找出规律解决问题.

练习册系列答案
相关题目