题目内容
7.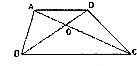 胜利公园前面有一块梯形停车场,如图,图中三角形ABC的面积是253平方米,三角形BOC的面积比三角形AOD的面积大42平方米,问停车场的面积是多少平方米?
胜利公园前面有一块梯形停车场,如图,图中三角形ABC的面积是253平方米,三角形BOC的面积比三角形AOD的面积大42平方米,问停车场的面积是多少平方米?
分析 由题意可知:三角形BOC的面积比三角形AOD的面积大42平方米,则三角形BOC的面积等于三角形AOD的面积加上42平方米,又因三角形BOC和三角形AOB的面积之和是253平方米,从而可以得出三角形AOB和三角形AOD的面积之和是253-42=211平方米,又因三角形DOC和三角形AOB的面积相等,所以可以得出三角形DOC和三角形AOD的面积之和也是211平方米,而梯形的面积等于三角形ABC和三角形ADC的面积之和,于是可以得出梯形的面积为253+211=464平方米,据此解答即可.
解答 解:由S△BOC-S△AOD=42可得:
S△BOC=S△AOD+42;
又因S△AOB+S△BOC=253,
即S△AOB+S△AOD+42=253,
所以SAOB+S△AOD
=253-42
=211;
又因S△AOB=S△DOC,
所以S△DOC+S△AOD=211,
所以梯形的面积
=S△ABC+S△ADC
=253+211
=464(平方米).
答:停车场的面积是464平方米.
点评 解答此题的关键是:利用等量代换的方法,以及三角形的面积之间的关系进行推理,即可得解.

练习册系列答案
相关题目
19.养殖场共养家禽1200只,其中鸡的只数占总只数的$\frac{2}{3}$,鸭的只数是鸡的只数的$\frac{1}{2}$.要求出鸡的只数,不需要的已知条件是( )
| A. | 养殖场共养家禽1200只 | B. | 鸡的只数占总只数的$\frac{2}{3}$ | ||
| C. | 鸭的只数是鸡的只数$\frac{1}{2}$ |
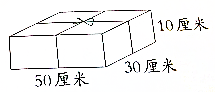 奶奶要过生日了,妈妈买了一个长50cm、宽30cm、高10cm的礼盒,里面装有奶奶爱吃的花生酥.礼盒用美丽的彩带扎一圈,打结处用去彩带15cm.这条彩带长约多少厘米?
奶奶要过生日了,妈妈买了一个长50cm、宽30cm、高10cm的礼盒,里面装有奶奶爱吃的花生酥.礼盒用美丽的彩带扎一圈,打结处用去彩带15cm.这条彩带长约多少厘米?