题目内容
 操作题:
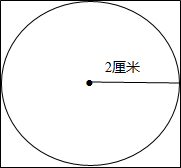
操作题:(1)在方框内画一个周长12.56厘米的圆;
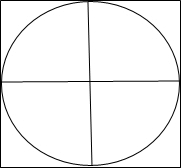
(2)在所画圆中,画两条相互垂直的直径;
(3)依次连接这两条直径的四个端点,得到一个正方形
(4)求这个正方形的面积是多少平方厘米?
分析:(1)根据题意,可利用圆的周长公式C=2πr计算出所画圆的半径,然后再进行作图即可;
(2)根据题意,可先作圆的一条直径,然后再作另一条直径,使两条直径相互垂直即可;
(3)顺次连接两条直径的端点即可得到一个圆内的最大正方形;
(4)可把圆内最大正方形的平均分为2个三角形,2个小三角形的底为圆的直径、高都为圆的半径,然后再根据三角形的面积公式计算出正方形的面积即可.
(2)根据题意,可先作圆的一条直径,然后再作另一条直径,使两条直径相互垂直即可;
(3)顺次连接两条直径的端点即可得到一个圆内的最大正方形;
(4)可把圆内最大正方形的平均分为2个三角形,2个小三角形的底为圆的直径、高都为圆的半径,然后再根据三角形的面积公式计算出正方形的面积即可.
解答:解:(1)圆的半径为:12.56÷3.14÷2=2(厘米),
作图如下:
(2)
(3)
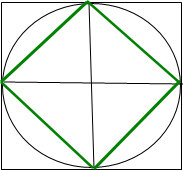
(4)正方形的面积为:4×2÷2×2=8(平方厘米),
答:正方形的面积是8平方厘米.
作图如下:

(2)

(3)

(4)正方形的面积为:4×2÷2×2=8(平方厘米),
答:正方形的面积是8平方厘米.
点评:此题主要考查的是在正方形内画圆、及其圆的周长公式的灵活应用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 操作题:
操作题: