题目内容
【题目】（4分）如图：三角形ABC的面积是31.2平方厘米．圆的直径AC=6cm，BD：DC=2：1，则阴影部分面积为 ．
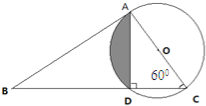
【答案】4.22平方厘米
【解析】
试题分析：连接OD，阴影部分的面积就是扇形AOD的面积减去三角形AOD的面积，分别求出扇形AOD的面积和三角形AOD的面积即可．
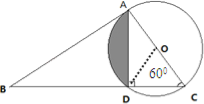
解：圆心角AOD的度数为180°﹣（180°﹣60°×2）=120°（度）
扇形AOD的面积为：（6÷2）2×3.14×
=3.14×9×
=9.42（平方厘米）
因为BD：DC=2：1，所以DC=BC，
那么三角形ADC的面积=三角形ABC的面积
又因为三角形AOD的面积与三角形ODC的面积相等（等底同高）
所以，阴影部分的面积为：9.42﹣31.2××
=9.42﹣5.2
=4.22（平方厘米）
答：阴影部分的面积是4.22平方厘米．
故答案为：4.22平方厘米．
练习册系列答案
相关题目
