题目内容
一个长为12厘米,宽为6厘米,高为3厘米的长方体内,挖去一个最大的圆锥体,这个圆锥体的体积最大是 立方厘米.
分析:削出的圆锥的方法有三种情况:
(1)以3厘米为底面直径,6厘米为高;
(2)以3厘米为底面直径,12厘米为高;
(3)以6厘米为底面直径,3厘米为高,由此利用圆锥的体积公式分别计算出它们的体积即可解答.
(1)以3厘米为底面直径,6厘米为高;
(2)以3厘米为底面直径,12厘米为高;
(3)以6厘米为底面直径,3厘米为高,由此利用圆锥的体积公式分别计算出它们的体积即可解答.
解答:解:①
×3.14×(3÷2)×6=14.13(平方厘米);
②
×3.14×(3÷2)×12=28.26(平方厘米);
③
×3.14×(6÷2)×3=28.26(立方厘米);
答:这个圆锥体的体积最大是28.26立方厘米.
故答案为:28.26.
| 1 |
| 3 |
②
| 1 |
| 3 |
③
| 1 |
| 3 |
答:这个圆锥体的体积最大是28.26立方厘米.
故答案为:28.26.
点评:解答此题的关键是,如何将一个长方体削成一个最大的圆锥,并找出它们之间的联系,再根据相应的公式解决问题.

练习册系列答案
相关题目
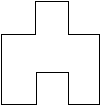 一个长为12厘米,宽为10厘米的长方形,挖去一个边长为4厘米的正方形补在另一边上(如图).所得图形的周长为
一个长为12厘米,宽为10厘米的长方形,挖去一个边长为4厘米的正方形补在另一边上(如图).所得图形的周长为