��Ŀ����
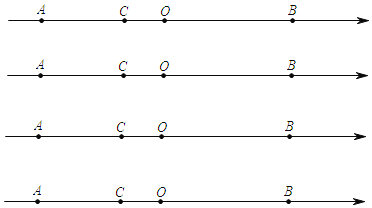
����Ŀ����ͼ������������A��B��C���㣬A��B��������ʾ���������ֱ���2k��4�ͩ�2k+4����kΪ���ĸ���������C��A��B֮�䣬��C��B�ľ����ǵ�A������2��������P�ӵ�A��������ÿ��3����λ���ȵ��ٶ������˶��������B���������أ���ÿ��3����λ���ȵ��ٶ������˶�������Q�ӵ�C��������ÿ��l����λ���ȵ��ٶ������˶���������ͬʱ�������˶�ʱ��Ϊt�룬����P���Q�ڶ����غ�ʱ��P��Q����ֹͣ�˶���
��1��ֱ��д��A��B��C��������������ֵ��A���� ��B���� ��C���� ��
��2����tΪ��ֵʱ��P����A���Q�ľ�����ȣ�
��3����tΪ��ֵʱ��P��Q�����ľ���Ϊ1����λ���ȣ�
���𰸡���1����6��6����2
��2��![]()
��3��![]() ��
��![]() ��
��![]()
��������
�⣺��1����kΪ���ĸ�������
��k����1��
���A��ʾ����Ϊ��6����B��ʾ����Ϊ6��
�֡ߵ�C��A��B֮�䣬��C��B�ľ����ǵ�A������2����
���C��ʾ����Ϊ��6+![]() ����2��
����2��
�ʴ�Ϊ����6��6����2��
��2�������⣬�ã���6+3t������6������2+t������6+3t����
��ã�t��![]() ��
��
�𣺵�tΪ![]() ʱ��P����A���Q�ľ�����ȣ�
ʱ��P����A���Q�ľ�����ȣ�
��3����P�����B��ʱ��Ϊ[6������6��]��3��4���룩��
����P�����Bʱ����Q��ʾ����Ϊ��2+4��2��
��P��Q�ڶ���������ʱ��Ϊ4+![]() ��5���룩��
��5���룩��
��0��t��4ʱ����P��ʾ����Ϊ��6+3t����Q��ʾ����Ϊ��2+t��
��PQ��1��
�ੁ2+t������6+3t����1��6+3t������2+t����1��
��ã�t��![]() ��t��
��t��![]() ��
��
��4��t��5ʱ����P��ʾ����Ϊ6��3��t��4������Q��ʾ����Ϊ��2+t��
��PQ��1��
��6��3��t��4��������2+t����1��
��ã�t��![]() ��
��
�𣺵�t��![]() ��
��![]() ��
��![]() ʱ��P��Q�����ľ���Ϊ1����λ���ȣ�
ʱ��P��Q�����ľ���Ϊ1����λ���ȣ�

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�