题目内容
(1)如图1中,甲、乙两个图形重叠部分的面积相当于甲面积 ,相当于乙面积的
,相当于乙面积的 .甲、乙两个图形的面积比是多少?
.甲、乙两个图形的面积比是多少?
(2)如图2,AO3= AB,AO2=
AB,AO2= AO3,阴影甲与阴影乙的面积的比多少?
AO3,阴影甲与阴影乙的面积的比多少?
(3)如图3,AB= AD,EC=
AD,EC= ED,图中阴影部分与空白部分面积的比多少?
ED,图中阴影部分与空白部分面积的比多少?
(4)如图4,S甲=16,S乙=12,S丙=10,阴影部分的面积是多少?

解:(1)重叠部分的面积=甲面积× ,则甲面积=重叠部分面积÷
,则甲面积=重叠部分面积÷ ;
;
重叠部分的面积=乙面积× ,则乙面积=重叠部分的面积÷
,则乙面积=重叠部分的面积÷ ;
;
所以甲面积:乙面积,
=(重叠部分面积÷ ):(重叠部分的面积÷
):(重叠部分的面积÷ );
);
=(重叠部分面积× ):(重叠部分的面积×
):(重叠部分的面积× )
)
= :
: ,
,
=( ×8):(
×8):( ×8),
×8),
=18:15,
=6:5;
答:甲、乙两个图形的面积比是6:5.
(2)阴影部分甲的面积=大圆面积-中圆的面积=π(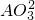 -
-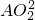 )=π[
)=π[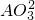 -
-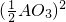 ]=
]= π
π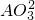 =
= π×(2AO2)2=3π
π×(2AO2)2=3π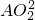 ;
;
阴影乙的面积=中圆的面积-小圆的面积=π(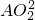 -
- )=π[
)=π[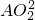 -
-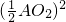 ]=
]= π
π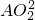 ;
;
所以甲面积:乙面积=3π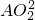 :
: π
π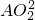 =3:
=3: =4:1.
=4:1.
答:阴影甲与阴影乙的面积的比是4:1.
(3)因为AB= AD,EC=
AD,EC= ED,
ED,
所以阴影部分的面积= 三角形ACD的面积;
三角形ACD的面积;
三角形ACD的面积= 三角形ABC的面积,
三角形ABC的面积,
所以阴影部分的面积= ×
× 三角形ABC的面积=
三角形ABC的面积= 三角形ABC的面积,
三角形ABC的面积,
所以阴影部分的面积:空白处的面积=1:7.
(4)由题意得:如图所示:
 ,
,
甲面积=ax=16,乙面积=ay=12,丙面积=by=10,
因为ay:by=12:10=6:5,所以b= a,
a,
则阴影三角形的面积=bx÷2,
= ax÷2,
ax÷2,
=甲面积× ÷2,
÷2,
=16× ×
× ,
,
= .
.
答:阴影部分的面积是 .
.
分析:(1)因为重叠部分的面积=甲面积× ,则甲面积=重叠部分面积÷
,则甲面积=重叠部分面积÷ ;重叠部分的面积=乙面积×
;重叠部分的面积=乙面积× ,则乙面积=重叠部分的面积÷
,则乙面积=重叠部分的面积÷ ,二者求比即可;
,二者求比即可;
(2)由题意得:阴影部分甲的面积=大圆面积-中圆的面积=π(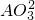 -
-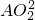 );阴影乙的面积=中圆的面积-小圆的面积=π(
);阴影乙的面积=中圆的面积-小圆的面积=π(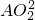 -
- ),代数计算即可;
),代数计算即可;
(3)因为AB= AD,EC=
AD,EC= ED,根据高一定时,三角形的面积与底成正比例的性质可得:阴影部分的面积=
ED,根据高一定时,三角形的面积与底成正比例的性质可得:阴影部分的面积= 三角形ACD的面积;三角形ACD的面积=
三角形ACD的面积;三角形ACD的面积= 三角形ABC的面积,由此可得:阴影部分的面积=
三角形ABC的面积,由此可得:阴影部分的面积= ×
× 三角形ABC的面积=
三角形ABC的面积= 三角形ABC的面积,由此即可解答.
三角形ABC的面积,由此即可解答.
(4)如图所示: ,甲面积=ax=16,乙面积=ay=12,丙面积=by=10,阴影三角形面积=bx÷2,又因为ay:by=12:10=6:5,所以b=
,甲面积=ax=16,乙面积=ay=12,丙面积=by=10,阴影三角形面积=bx÷2,又因为ay:by=12:10=6:5,所以b= a,则bx=
a,则bx= ax,则三角形的面积=甲面积×
ax,则三角形的面积=甲面积× ,计算即可.
,计算即可.
点评:(1)解决本题的关键是将两个图形的面积借助中间量表示出来,再求比;
(2)解决本题的关键是借助半径之间的关系求比;
(3)此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.
(4)解决本题的关键是表示出各个图形的面积,再转换计算.
 ,则甲面积=重叠部分面积÷
,则甲面积=重叠部分面积÷ ;
;重叠部分的面积=乙面积×
 ,则乙面积=重叠部分的面积÷
,则乙面积=重叠部分的面积÷ ;
;所以甲面积:乙面积,
=(重叠部分面积÷
 ):(重叠部分的面积÷
):(重叠部分的面积÷ );
);=(重叠部分面积×
 ):(重叠部分的面积×
):(重叠部分的面积× )
)=
 :
: ,
,=(
 ×8):(
×8):( ×8),
×8),=18:15,
=6:5;
答:甲、乙两个图形的面积比是6:5.
(2)阴影部分甲的面积=大圆面积-中圆的面积=π(
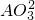 -
-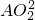 )=π[
)=π[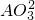 -
-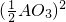 ]=
]= π
π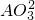 =
= π×(2AO2)2=3π
π×(2AO2)2=3π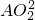 ;
;阴影乙的面积=中圆的面积-小圆的面积=π(
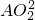 -
- )=π[
)=π[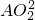 -
-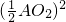 ]=
]= π
π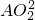 ;
;所以甲面积:乙面积=3π
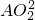 :
: π
π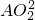 =3:
=3: =4:1.
=4:1.答:阴影甲与阴影乙的面积的比是4:1.
(3)因为AB=
 AD,EC=
AD,EC= ED,
ED,所以阴影部分的面积=
 三角形ACD的面积;
三角形ACD的面积;三角形ACD的面积=
 三角形ABC的面积,
三角形ABC的面积,所以阴影部分的面积=
 ×
× 三角形ABC的面积=
三角形ABC的面积= 三角形ABC的面积,
三角形ABC的面积,所以阴影部分的面积:空白处的面积=1:7.
(4)由题意得:如图所示:
 ,
,甲面积=ax=16,乙面积=ay=12,丙面积=by=10,
因为ay:by=12:10=6:5,所以b=
 a,
a,则阴影三角形的面积=bx÷2,
=
 ax÷2,
ax÷2,=甲面积×
 ÷2,
÷2,=16×
 ×
× ,
,=
 .
.答:阴影部分的面积是
 .
.分析:(1)因为重叠部分的面积=甲面积×
 ,则甲面积=重叠部分面积÷
,则甲面积=重叠部分面积÷ ;重叠部分的面积=乙面积×
;重叠部分的面积=乙面积× ,则乙面积=重叠部分的面积÷
,则乙面积=重叠部分的面积÷ ,二者求比即可;
,二者求比即可;(2)由题意得:阴影部分甲的面积=大圆面积-中圆的面积=π(
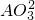 -
-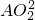 );阴影乙的面积=中圆的面积-小圆的面积=π(
);阴影乙的面积=中圆的面积-小圆的面积=π(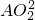 -
- ),代数计算即可;
),代数计算即可;(3)因为AB=
 AD,EC=
AD,EC= ED,根据高一定时,三角形的面积与底成正比例的性质可得:阴影部分的面积=
ED,根据高一定时,三角形的面积与底成正比例的性质可得:阴影部分的面积= 三角形ACD的面积;三角形ACD的面积=
三角形ACD的面积;三角形ACD的面积= 三角形ABC的面积,由此可得:阴影部分的面积=
三角形ABC的面积,由此可得:阴影部分的面积= ×
× 三角形ABC的面积=
三角形ABC的面积= 三角形ABC的面积,由此即可解答.
三角形ABC的面积,由此即可解答.(4)如图所示:
 ,甲面积=ax=16,乙面积=ay=12,丙面积=by=10,阴影三角形面积=bx÷2,又因为ay:by=12:10=6:5,所以b=
,甲面积=ax=16,乙面积=ay=12,丙面积=by=10,阴影三角形面积=bx÷2,又因为ay:by=12:10=6:5,所以b= a,则bx=
a,则bx= ax,则三角形的面积=甲面积×
ax,则三角形的面积=甲面积× ,计算即可.
,计算即可.点评:(1)解决本题的关键是将两个图形的面积借助中间量表示出来,再求比;
(2)解决本题的关键是借助半径之间的关系求比;
(3)此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.
(4)解决本题的关键是表示出各个图形的面积,再转换计算.

练习册系列答案
相关题目


 (2011?秀屿区)如图是科技大赛中两个机器人赛跑的路程与时间关系的图象.
(2011?秀屿区)如图是科技大赛中两个机器人赛跑的路程与时间关系的图象.