题目内容
| 简算. 41  × × +51 +51 × × |  ×39+ ×39+ ×27 ×27 | 238÷238 |
54 ÷17 ÷17 | (9 +7 +7 )÷( )÷( + + ) ) |  × × + + × ×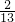 + + × ×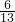 . . |
解:(1)41 ×
× +51
+51 ×
× ,
,
=(40+1 )×
)× +(50+1
+(50+1 )×
)× ,
,
=40× +
+ ×
× +50×
+50× +
+ ×
× ,
,
=30+1+40+1,
=72;
(2) ×39+
×39+ ×27,
×27,
= ×
× ×39+
×39+ ×27,
×27,
=( ×39+27)×
×39+27)× ,
,
=(13+27)× ,
,
=40× ,
,
=30;
(3)238÷238 ,
,
=238÷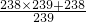 ,
,
=238×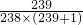 ,
,
=238×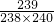 ,
,
=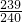 ;
;
(4)54 ÷17,
÷17,
=(51+3 )÷17,
)÷17,
=51÷17+ ÷17,
÷17,
=3+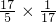 ,
,
=3+ ,
,
=3 ;
;
(5)(9 +7
+7 )÷(
)÷( +
+ ),
),
=(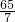 +
+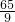 )÷(
)÷( +
+ ),
),
=( +
+ )×65÷[(
)×65÷[( +
+ )×5],
)×5],
=65÷5,
=13;
(6) ×
× +
+ ×
×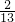 +
+ ×
×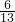 ,
,
= ×
× +
+ ×
× +
+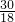 ×
× ,
,
=( +
+ +
+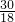 )×
)× ,
,
=( +
+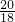 +
+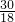 )×
)× ,
,
=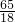 ×
× ,
,
= .
.
分析:(1)把41 拆成40+1
拆成40+1 ,51
,51 拆成50+1
拆成50+1 ,运用乘法分配律简算;
,运用乘法分配律简算;
(2)为了简算,把原式变为 ×
× ×39+
×39+ ×27,然后运用乘法分配律的逆运算计算;
×27,然后运用乘法分配律的逆运算计算;
(3)先把238 化为假分数,在化假分数的过程中,不要先把分子的结果算出来,因为在改为乘法运算时,分母中的238能与被除数238约分,得以简算;
化为假分数,在化假分数的过程中,不要先把分子的结果算出来,因为在改为乘法运算时,分母中的238能与被除数238约分,得以简算;
(4)根据数字特点,把54 拆分为(51+3
拆分为(51+3 ),运用除法的性质简算;
),运用除法的性质简算;
(5)先把第一个括号内的分数化为假分数,发现分子相同,于是可把原式变为( +
+ )×65÷[(
)×65÷[( +
+ )×5],然后通过约分、计算即可;
)×5],然后通过约分、计算即可;
(6)根据数字特点,把原式变为 ×
× +
+ ×
× +
+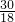 ×
× ,运用乘法分配律的逆运算简算.
,运用乘法分配律的逆运算简算.
点评:此题主要考查运用运算定律或技巧,对分数、整数的四则混合运算的简算能力.
 ×
× +51
+51 ×
× ,
,=(40+1
 )×
)× +(50+1
+(50+1 )×
)× ,
,=40×
 +
+ ×
× +50×
+50× +
+ ×
× ,
,=30+1+40+1,
=72;
(2)
 ×39+
×39+ ×27,
×27,=
 ×
× ×39+
×39+ ×27,
×27,=(
 ×39+27)×
×39+27)× ,
,=(13+27)×
 ,
,=40×
 ,
,=30;
(3)238÷238
 ,
,=238÷
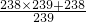 ,
,=238×
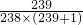 ,
,=238×
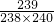 ,
,=
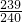 ;
;(4)54
 ÷17,
÷17,=(51+3
 )÷17,
)÷17,=51÷17+
 ÷17,
÷17,=3+
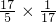 ,
,=3+
 ,
,=3
 ;
;(5)(9
 +7
+7 )÷(
)÷( +
+ ),
),=(
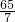 +
+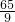 )÷(
)÷( +
+ ),
),=(
 +
+ )×65÷[(
)×65÷[( +
+ )×5],
)×5],=65÷5,
=13;
(6)
 ×
× +
+ ×
×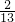 +
+ ×
×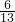 ,
,=
 ×
× +
+ ×
× +
+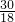 ×
× ,
,=(
 +
+ +
+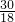 )×
)× ,
,=(
 +
+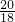 +
+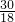 )×
)× ,
,=
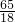 ×
× ,
,=
 .
.分析:(1)把41
 拆成40+1
拆成40+1 ,51
,51 拆成50+1
拆成50+1 ,运用乘法分配律简算;
,运用乘法分配律简算;(2)为了简算,把原式变为
 ×
× ×39+
×39+ ×27,然后运用乘法分配律的逆运算计算;
×27,然后运用乘法分配律的逆运算计算;(3)先把238
 化为假分数,在化假分数的过程中,不要先把分子的结果算出来,因为在改为乘法运算时,分母中的238能与被除数238约分,得以简算;
化为假分数,在化假分数的过程中,不要先把分子的结果算出来,因为在改为乘法运算时,分母中的238能与被除数238约分,得以简算;(4)根据数字特点,把54
 拆分为(51+3
拆分为(51+3 ),运用除法的性质简算;
),运用除法的性质简算;(5)先把第一个括号内的分数化为假分数,发现分子相同,于是可把原式变为(
 +
+ )×65÷[(
)×65÷[( +
+ )×5],然后通过约分、计算即可;
)×5],然后通过约分、计算即可;(6)根据数字特点,把原式变为
 ×
× +
+ ×
× +
+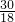 ×
× ,运用乘法分配律的逆运算简算.
,运用乘法分配律的逆运算简算.点评:此题主要考查运用运算定律或技巧,对分数、整数的四则混合运算的简算能力.

练习册系列答案
相关题目
用递等式计算,能简算的要简算.
(1)2-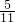 ÷ ÷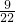 - - | (2)6÷[( + + )× )×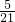 ] ] | (3)(41×9.9+4.1) |
(4)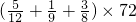 | (5)754-(302+459÷51) | (6)9×( - - )×13. )×13. |