题目内容
【题目】图形计算。（本题7分）
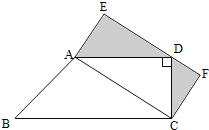
如图，ABCD是直角梯形，ACFE是长方形，已知BC﹣AD=4cm，CD=6cm，梯形面积是60cm2，求阴影部分的面积．
【答案】阴影部分的面积是24cm2
【解析】
分析：首先根据梯形的面积是60cm2，高是6cm，求出梯形的上底和下底的和，进而求出梯形的上底和下底分别是多少；然后判断出阴影部分的面积等于三角形ACD的面积，求出三角形ACD的面积，即可求出阴影部分的面积是多少．
解：BC+AD=（60×2）÷6=20cm…①，
BC﹣AD=4cm…②，
由①②，可得
BC=12cm，AD=8cm；
因为三角形ACD的面积等于AC的乘以CF，再除以2，
所以三角形ACD的面积等于长方形ACFE的面积的一半，
因此阴影部分的面积等于三角形ACD的面积，
则阴影部分的面积=AD×CD÷2=8×6÷2=24（cm2）．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】下面是二年二班同学阅读课上阅读图书情况统计表，请同学们仔细观察下表，并回答问题。
阅读图书种类 | 童话故事 | 十万个为什么 | 寓言故事 | 成语故事 |
阅读人数 | 8 | 16 | 6 | 10 |
（1）喜欢阅读________的人数最多，喜欢阅读________人数最少.
（2）二年二班一共有________人。
（3）学校图书室响购买一批新书，你有什么好的建议________。