题目内容
看图填数.
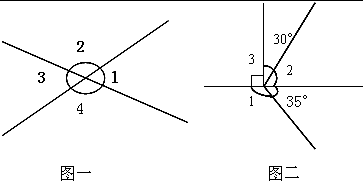
①如图一,已知∠1=75°,那么∠2=
②如图二,∠1=

①如图一,已知∠1=75°,那么∠2=
105°
105°
∠3=75°
75°
∠4=105°
105°
. ②如图二,∠1=
145°
145°
∠2=60°
60°
∠3=90°
90°
.分析:(1)我们通过给出的已知条件,进行画图解答,由图可知∠1与∠3,∠2与∠4,分别是对顶角,根据对顶角的性质进行解答即可.
(2)由图可知∠1加上35°等于180°,∠2加上30°等于90°,∠3是一个直角是90°.
(2)由图可知∠1加上35°等于180°,∠2加上30°等于90°,∠3是一个直角是90°.
解答:解:因为∠1+∠2=180°,∠1=75°,
所以75°+∠2=180°,
75°-75°+∠2=180°-75°,
∠2=105°;
因为∠1与∠3,∠2与∠4,分别是对顶角,
所以∠1=∠3=75°,∠2=∠4=105°;
(2)因为∠1+35°=180°,
∠1+35°-35°=180°-35°,
∠1=145°;
因为∠2+30°=90°,
∠2+30°-30°=90°-30°,
∠2=60°;
因为∠3是一个直角,
所以∠3=90°;
故答案为:(1)105°,75°,105°.(2)145°,60°,90°.
所以75°+∠2=180°,
75°-75°+∠2=180°-75°,
∠2=105°;
因为∠1与∠3,∠2与∠4,分别是对顶角,
所以∠1=∠3=75°,∠2=∠4=105°;
(2)因为∠1+35°=180°,
∠1+35°-35°=180°-35°,
∠1=145°;
因为∠2+30°=90°,
∠2+30°-30°=90°-30°,
∠2=60°;
因为∠3是一个直角,
所以∠3=90°;
故答案为:(1)105°,75°,105°.(2)145°,60°,90°.
点评:本题运用对顶角的意义、余角及补角的定义进行解答即可.

练习册系列答案
相关题目
 想一想
想一想
 想一想
想一想