题目内容
在“前面的横线”里写出每组数的最小公倍数,在“后面的横线”里写出每组数的最大公因数.
3和9 12和11 17和85
12和15 60和45 2和13 .
3和9
12和15
分析:根据求两个数最大公约数也就是这两个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数的连乘积求解
解答:解:9=3×3
所以3和9的最小公倍数是9,最大公因数是3;
12和11互质,所以12和11的最小公倍数是12×11=132,最大公因数是1;
85=17×3,
所以17和85的最小公倍数是85,最大公因数是17;
12=3×2×2
15=3×5
所以12和15的最小公倍数是3×2×2×5=60,最大公因数是3;
60=2×2×3×5
45=3×3×5
所以60和45的最小公倍数是3×5×2×2×3=180,最大公因数是3×5=15;
2和13互质,
所以2和13的最小公倍数是2×13=26,最大公因数是1.
故答案为:9,3;132,11;85,17;60,3;180,15;26,1.
所以3和9的最小公倍数是9,最大公因数是3;
12和11互质,所以12和11的最小公倍数是12×11=132,最大公因数是1;
85=17×3,
所以17和85的最小公倍数是85,最大公因数是17;
12=3×2×2
15=3×5
所以12和15的最小公倍数是3×2×2×5=60,最大公因数是3;
60=2×2×3×5
45=3×3×5
所以60和45的最小公倍数是3×5×2×2×3=180,最大公因数是3×5=15;
2和13互质,
所以2和13的最小公倍数是2×13=26,最大公因数是1.
故答案为:9,3;132,11;85,17;60,3;180,15;26,1.
点评:考查了求几个数的最大公因数的方法与最小公倍数的方法:两个数的公有质因数连乘积是最大公约数;两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除法解答.

练习册系列答案
相关题目

 ________;1________; 0.2________;
________;1________; 0.2________;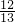 ________;
________;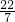 ________;
________; ________.
________.