题目内容
1. 如图所示,AD=$\frac{1}{2}$DC,AE=BE,那么三角形ABC的面积是三角形ADE面积的( )倍.
如图所示,AD=$\frac{1}{2}$DC,AE=BE,那么三角形ABC的面积是三角形ADE面积的( )倍.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 首先根据AD=$\frac{1}{2}$DC,应用三角形的面积和底的正比关系,判断出出:${S}_{△ABD}={\frac{1}{3}S}_{△ABC}$;然后根据AE=BE,判断出${S}_{△ADE}={\frac{1}{2}S}_{△ABD}$,进而判断出三角形ABC的面积是三角形ADE面积的多少倍即可.
解答 解:如图,连接BD,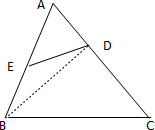 ,
,
因为AD=$\frac{1}{2}$DC,
所以${S}_{△ABD}={\frac{1}{2}S}_{△BCD}={\frac{1}{3}S}_{△ABC}$,
因为AE=BE,
所以${S}_{△ADE}={\frac{1}{2}S}_{△ABD}=\frac{1}{2}×{\frac{1}{3}S}_{△ABC}=\frac{1}{6}$S△ABC,
所以S△ABC=6S△ADE,
即三角形ABC的面积是三角形ADE面积的6倍.
故选:A.
点评 此题主要考查了三角形的面积和底的正比关系,要熟练掌握,解答此题的关键是判断出:${S}_{△ABD}={\frac{1}{3}S}_{△ABC}$.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.育红小学春季植树情况统计表,请你把它填写完整.
育红小学四、五年级植树情况统计表 2000年4月
五年级植树棵数高于平均每班植树棵数.
育红小学四、五年级植树情况统计表 2000年4月
| 年级 | 班级 | 植树棵数 | 平均每班植树棵数 |
| 合计 | |||
| 四年级 | 2 | 80 | |
| 五年级 | 3 | 45 |
 在(虚线框内)画一个底角是45°、高是2厘米,面积是8平方厘米的直角梯形.
在(虚线框内)画一个底角是45°、高是2厘米,面积是8平方厘米的直角梯形. 读图填空.
读图填空.