题目内容
13.如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));以此下去…,求正方形A4B4C4D4的面积?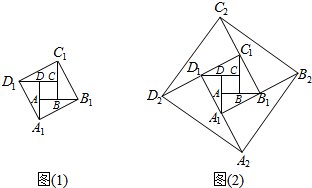
分析 本题需先根据已知条件得出延长n次时面积的公式,再根据求正方形A4B4C4D4正好是要求的第5次的面积,把它代入即可求出答案.在直角三角形CC1中,CD1=2,CC1=1,运用勾股定理可求得C1D1=$\sqrt{5}$,所以延长一次为$\sqrt{5}$,面积为5,再延长为51=5,面积52=25,…,据此解答即可.
解答 解:最初边长为1,面积为1,
在直角三角形CC1中,CD1=2,CC1=1,
则(C1D1)2=(CC1)2+(CD1)2
=12+22
=1+4
=5
C1D1=$\sqrt{5}$,
所以延长一次为$\sqrt{5}$,面积为5,
再延长为51=5,面积52=25,…,
下一次延长为5$\sqrt{5}$,面积53=125,
以此类推,
当N=4时,正方形A4B4C4D4的面积为:54=625.
答:正方形A4B4C4D4的面积为625.
点评 本题主要考查了正方形的性质,在解题时要根据已知条件找出规律,从而得出正方形的面积,这是一道常考题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
3.有2厘米、7厘米、14厘米的小棒各2根,选其中的3根围成一个三角形,周长最短是( )厘米.
| A. | 11 | B. | 16 | C. | 28 | D. | 35 |
8.红星区2007~2011年新增手机用户情况如下表.
(1)根据以上数据绘制下面的折线统计图.
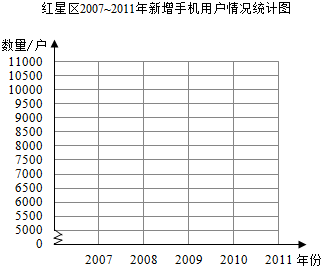
(2)根据统计图回答问题.
?红星区2011年新增手机用户是多少?
这5年来,红星区平均每年新增手机用户多少户?你还能得到哪些信息?
| 年份 | 2007 | 2008 | 2009 | 2010 | 201 |
| 数量/户 | 5500 | 6800 | 10500 | 9000 | 8000 |

(2)根据统计图回答问题.
?红星区2011年新增手机用户是多少?
这5年来,红星区平均每年新增手机用户多少户?你还能得到哪些信息?