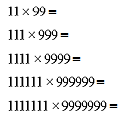题目内容
| 先计算前两个算式,用发现的规律计算下面各题. 51×61= |
81×71= | 91×41= |
| 61×31= | 21×91= | 41×51= |
分析:先算出前两个算式的积,观察算式发现,都是两位因数乘两位因数且个位上都是1,再看积:是四位数,尾数是1,前两位是因数最高位的两个数字的乘积,中间两位再加上最高位的两个数字的和;据此规律解答即可.
解答:解:51×61=3111=50×60+(5+6)×10+1或3(0+1)11
81×71=5751=80×70+(8+7)×10+1或5(6+1)51
91×41=3600+130+1=3731或3(6+1)31
61×31=1(8+0)91=1891
21×91=1(8+1)11=1911
41×51=2(0+0)91=2091
81×71=5751=80×70+(8+7)×10+1或5(6+1)51
91×41=3600+130+1=3731或3(6+1)31
61×31=1(8+0)91=1891
21×91=1(8+1)11=1911
41×51=2(0+0)91=2091
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| 先用竖式计算下面四个算式的积,然后进行观察: (1)相乘的两个数十位上数、个位上数各有何特点? (2)若将积分为后两位和前两位,请你探索后两位数与乘数个位数有何联系?前两位数与乘数的十位数有什么联系?把你的发现写下来,并利用你的发现很快写出后4道乘法算式的积。 | ||||
| ||||
|