题目内容
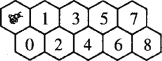
【题目】一排蜂房编号如图所示,左上角有一只小蜜蜂,还不会飞.只会向前爬行,它爬行到8号蜂房,共有________种路线.
【答案】55
【解析】
解法一、画树状图分析。

观察图形可以得出,共有55种不同的路线。
解法二、利用斐波那契数列解决。
按规则,蜜蜂从最初位置到0号蜂房只有唯一的一种爬法。从最初位置到1号蜂房有2种不同爬法:蜜蜂→1号;蜜蜂→0号→1号。同理,蜜蜂从最初位置到2号蜂房有3种不同爬法:蜜蜂→0号→2号;蜜蜂→1号→2号;蜜蜂→0号→1号→2号。从最初位置到3号蜂房有5种不同爬法:蜜蜂→1号→3号;蜜蜂→0号→2号→3号;蜜蜂→0号→1号→2号→3号;蜜蜂→1号→2号→3号;蜜蜂→0号→1号→3号。容易得出:蜜蜂要是想从最初位置爬到4号蜂房,那它在到4号蜂房之前,最后一个落脚点不是2号蜂房就是3号蜂房。所以蜜蜂从最初位置到4号蜂房的不同爬法的总数,就是它从最初位置到2号蜂房的不同爬法的总数与它从最初位置到3号蜂房的不同爬法的总数的和。因此蜜蜂从最初位置到4号蜂房的不同爬法的总数为3+5=8。以此类推,就会得到蜜蜂到达各蜂房的不同爬法总和分别是:1,2,3,5,8,13,21,34,55,89……
所以蜜蜂爬行到8号蜂房共有55种路线。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目