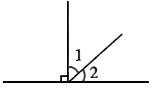
题目内容
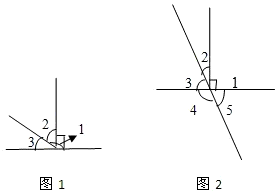 求出下面角的度数
求出下面角的度数
(1)图1,已知∠1=145°,则∠2、∠3分别是多少?
(2)图2,已知∠1=90°∠2=30°,则∠3;∠4;∠5分别是多少°.
解:(1)∠2=145-90=55(度);
∠3=180-145=35(度);
答:∠2是55度,∠3是35度.
(2)∠3=90-30=60(度);
∠4=180-60=120(度);
∠5=180-120=60(度);
答:∠3是60度,∠4是120度,∠5是60度.
分析:(1)观察图形可知:∠1是∠2与一个直角组成的角,所以可得∠2=145-90=55度;∠1与∠3组成了一个平角,所以∠3=180-145=35度,据此计算;
(2)观察图形可知:∠2与∠3组成一个直角,所以∠3=90-30=60度;∠3与∠4组成一个平角,所以∠4=180-60=120度;因为∠4与∠5组成一个平角,所以∠5=180-120=60度;由此计算即可解答.
点评:结合图形中的特殊角如:平角和直角,再利用特殊角的度数进行计算即可解答.
∠3=180-145=35(度);
答:∠2是55度,∠3是35度.
(2)∠3=90-30=60(度);
∠4=180-60=120(度);
∠5=180-120=60(度);
答:∠3是60度,∠4是120度,∠5是60度.
分析:(1)观察图形可知:∠1是∠2与一个直角组成的角,所以可得∠2=145-90=55度;∠1与∠3组成了一个平角,所以∠3=180-145=35度,据此计算;
(2)观察图形可知:∠2与∠3组成一个直角,所以∠3=90-30=60度;∠3与∠4组成一个平角,所以∠4=180-60=120度;因为∠4与∠5组成一个平角,所以∠5=180-120=60度;由此计算即可解答.
点评:结合图形中的特殊角如:平角和直角,再利用特殊角的度数进行计算即可解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
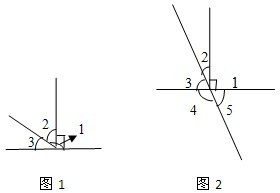 求出下面角的度数
求出下面角的度数