题目内容
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第10次“移位”后,则他所处顶点的编号是3
3
.分析:根据“移位”的特点确定出前几次的移位情况,从而找出规律,然后解答即可.
解答:解:根据题意,小宇从编号为2的顶点开始,第1次移位到点4,
第2次移位到达点3,
第3次移位到达点1,
第4次移位到达点2,
…,
依此类推,4次移位后回到出发点,
10÷4=2…2.
所以第10次移位为第3个循环组的第2次移位,到达点3.
故答案为:3.
第2次移位到达点3,
第3次移位到达点1,
第4次移位到达点2,
…,
依此类推,4次移位后回到出发点,
10÷4=2…2.
所以第10次移位为第3个循环组的第2次移位,到达点3.
故答案为:3.
点评:本题对图形变化规律的考查,根据“移位”的定义,找出每4次移位为一个循环组进行循环是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 以如图一点0作为角的顶点,画一个135度的角,并标出各部分的名称.
以如图一点0作为角的顶点,画一个135度的角,并标出各部分的名称.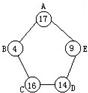 60个同学去野营,他们搭的五顶帐蓬正好位于正五边形的五个顶点上(见图),图中圆圈内的数字表示各个帐蓬内的人数.现在想将五个帐蓬内的人数调整为一样多,怎样调动最简便?
60个同学去野营,他们搭的五顶帐蓬正好位于正五边形的五个顶点上(见图),图中圆圈内的数字表示各个帐蓬内的人数.现在想将五个帐蓬内的人数调整为一样多,怎样调动最简便? 如图,每个圆的半径都是12厘米,正五边形的周长是多少厘米.
如图,每个圆的半径都是12厘米,正五边形的周长是多少厘米. 以如图一点0作为角的顶点,画一个135度的角,并标出各部分的名称.
以如图一点0作为角的顶点,画一个135度的角,并标出各部分的名称.