题目内容
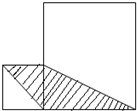 如图,左右两个正方形中的阴影部分的面积比是1:3,则空白部分的面积之比是
如图,左右两个正方形中的阴影部分的面积比是1:3,则空白部分的面积之比是分析:由题意知:两个正方形中阴影部分面积比是1:3,根据三角形的底一定时,三角形的面积与高成正比例的性质,可得:这两个三角形的高的比是1:3,即两个正方形的边长之比是1:3,由此设小正方形的边长是1,则大正方形的边长是3,由此利用正方形的面积公式即可算出这两个正方形的面积,则空白部分的面积等于每个正方形的面积去掉每个阴影部分的面积,从而算出它们的面积比.
解答:解:因为两个正方形中阴影部分面积比是1:3,可得:阴影部分的这两个三角形的高的比是1:3,即两个正方形的边长之比是1:3,
由此设小正方形的边长是1,则大正方形的边长是3,
则小正方形空白处的面积是:1×1÷2=
;
大正方形内空白处的面积是:3×3-3×1÷2=
,
所以它们的面积之比是:
:
=1:15,
故答案为:1:15.
由此设小正方形的边长是1,则大正方形的边长是3,
则小正方形空白处的面积是:1×1÷2=
| 1 |
| 2 |
大正方形内空白处的面积是:3×3-3×1÷2=
| 15 |
| 2 |
所以它们的面积之比是:
| 1 |
| 2 |
| 15 |
| 2 |
故答案为:1:15.
点评:此题解决的突破口在于先根据图形特点及两个阴影部分的比,找准两个正方形边的关系,利用赋值法,从而解决问题.

练习册系列答案
相关题目
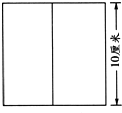 如图是一个正方形,边长是10厘米,如图从中间剪开,左右两个长方形的周长各是多少?两个长方形周长的和与原来正方形的周长相等吗?
如图是一个正方形,边长是10厘米,如图从中间剪开,左右两个长方形的周长各是多少?两个长方形周长的和与原来正方形的周长相等吗? 如图,左右两个正方形中的阴影部分的面积比是1:3,则空白部分的面积之比是________.
如图,左右两个正方形中的阴影部分的面积比是1:3,则空白部分的面积之比是________.