题目内容
如图,一个大正方形被两条线段分割成S1、S3两个小正方形和S2、S4两个长方形.已知S1=75平方厘米,S2=15平方厘米,求大正方形的面积是多少平方厘米?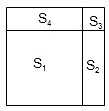
 解:S1=75平方厘米,S2=15平方厘米,
解:S1=75平方厘米,S2=15平方厘米,等高的矩形底边的比等于面积比,
BH:CH=75:15,即BH:CH=5,
则BH=5HC,
则BC=6HC,
可知BC=1.2BH,
由正方形的面积与边长的平方成正比例可知:
大正方形的面积为:
75×(1.2×1.2),
=75×1.44,
=108(平方厘米).
答:大正方形的面积是108平方厘米.
分析:由S1=75平方厘米,S2=15平方厘米,根据等高的矩形底边的比等于面积比,BH=5HC,可知BC=1.2BH,再根据正方形的面积公式:S=a2,可知大正方形的面积.
点评:本题考查了正方形、矩形面积的计算,计算正方形ABCD的边长与正方形S1的边长的关系并求面积是解题的关键.

练习册系列答案
相关题目
 (2006?徐州)如图是一个大正方形被平均分成9个小正方形.请你在这种分割下用阴影表示出大正方形的
(2006?徐州)如图是一个大正方形被平均分成9个小正方形.请你在这种分割下用阴影表示出大正方形的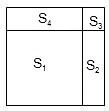 如图,一个大正方形被两条线段分割成S1、S3两个小正方形和S2、S4两个长方形.已知S1=75平方厘米,S2=15平方厘米,求大正方形的面积是多少平方厘米?
如图,一个大正方形被两条线段分割成S1、S3两个小正方形和S2、S4两个长方形.已知S1=75平方厘米,S2=15平方厘米,求大正方形的面积是多少平方厘米? 如图是一个大正方形被平均分成9个小正方形.请你在这种分割下用阴影表示出大正方形的
如图是一个大正方形被平均分成9个小正方形.请你在这种分割下用阴影表示出大正方形的 .
.