题目内容
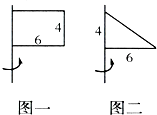 如图 (单位:厘米),绕轴旋转1周,图一得到
如图 (单位:厘米),绕轴旋转1周,图一得到圆柱
圆柱
体,体积是452.16
452.16
立方厘米;图二得到圆锥
圆锥
体,体积是150.72
150.72
立方厘米.分析:(1)根据圆柱展开图的特点可得:图一长方形以4厘米边为轴旋转一周得到的是一个圆柱,此时圆柱的高是4厘米,底面半径是6厘米,再利用圆柱的体积公式即可解决问题.
(2)根据圆锥展开图的特点可得:图二旋转后得到圆锥体,圆锥的底面半径是6厘米,高是4厘米,利用公式V圆锥=
Sh解答即可.
(2)根据圆锥展开图的特点可得:图二旋转后得到圆锥体,圆锥的底面半径是6厘米,高是4厘米,利用公式V圆锥=
| 1 |
| 3 |
解答:解:绕轴旋转1周,图一得到圆柱体,体积是:
3.14×62×4,
=3.14×144,
=452.16(立方厘米);
图二得到圆柱体,体积是:
×3.14×62×4,
=
×3.14×144,
=150.72(立方厘米);
故答案为:圆柱,452.16,圆锥,150.72.
3.14×62×4,
=3.14×144,
=452.16(立方厘米);
图二得到圆柱体,体积是:
| 1 |
| 3 |
=
| 1 |
| 3 |
=150.72(立方厘米);
故答案为:圆柱,452.16,圆锥,150.72.
点评:明确圆柱侧面展开图和圆锥侧面展开图的特点,灵活掌握圆锥、圆柱的体积计算公式,是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

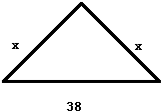 (2008?长汀县)如图(单位:厘米)中三角形的周长用含有字母的式子表示是
(2008?长汀县)如图(单位:厘米)中三角形的周长用含有字母的式子表示是 如图,长方形ABCD中放置了9个形状、大小都相同的小长方形(尺寸如图,单位:厘米),则图中阴影部分的面积为( )
如图,长方形ABCD中放置了9个形状、大小都相同的小长方形(尺寸如图,单位:厘米),则图中阴影部分的面积为( )