题目内容
2.(1)把三角形绕A点顺时针旋转90°,得到图形①.(2)点B的位置用数对表示是(10,12),以点B为圆心,画一个直径为2厘米的圆.
(3)画与平行四边形面积相等的一个长方形和一个三角形.
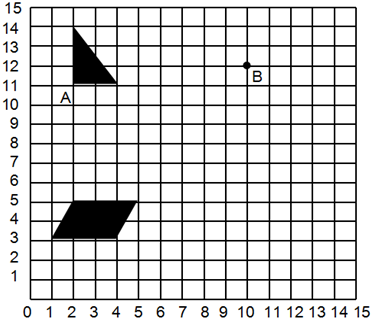
分析 (1)根据旋转的特征,三角形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形①.
(2)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点B的位置;再以B为圆心,以2厘米为直径画圆即可.
(3)图中平行四边形的面积是3×2=6(平方厘米),画一个长为3厘米、宽为2厘米的长方形,其面积是3×2=6(平方厘米);画一个底为3厘米、高为4厘米的三角形,其面积是3×4÷2=6(平方厘米).
解答 解:(1)把三角形绕A点顺时针旋转90°,得到图形①(下图):
(2)点B的位置用数对表示是(10,12),以点B为圆心,画一个直径为2厘米的圆(下图):
(3)画与平行四边形面积相等的一个长方形和一个三角形(下图):
故答案为:(10,12).
点评 此题考查的知识点有:作旋转一定度数后的图形,点与数对,平行四形、长方形、三角形面积的计算,根据面积画长方形、三角形,画圆等.

练习册系列答案
相关题目
12.直接写出得数.
| 36+9= | 85-32= | 38×4= | 360÷90= |
| 7.1+2.6= | 8-4.2= | 0.23= | 2.4×0.5= |
| 0.96÷0.02= | 3.7×1000= | $\frac{1}{2}$-$\frac{1}{4}$= | $\frac{1}{9}$+$\frac{5}{6}$= |
| $\frac{1}{3}$×$\frac{6}{7}$= | 81÷$\frac{9}{5}$= | $\frac{7}{15}$÷$\frac{4}{3}$= | 2-$\frac{4}{9}$= |
| $\frac{1}{3}$÷$\frac{2}{3}$= | 16×$\frac{3}{4}$= | $\frac{1}{4}$+0.75= | 1-96%= |
17.要表示同学们最喜欢的体育活动,应该选取( )
| A. | 平均数 | B. | 中位数 | C. | 众数 |
