题目内容
3.古希腊著名的数学家阿基米德是历史上最杰出的数学家之一.他发现了圆柱容球定理.当圆柱球时,球的直径与圆柱的高和底面直径相等.假设圆柱的底面半径为r,那么圆柱的体积V柱=πr2×2r=2πr3.阿基米德还证明了V球=$\frac{4}{3}$πr3所以$\frac{2}{3}$V柱=V球,也就是球的体积正好是圆柱体积的三分之二.阿基米德还发现,当圆柱容球时,球的表面积也是圆柱表面积的三分之二.如果一个圆柱的底面半径是4厘米,高是5厘米.你能求出球的表面积吗?分析 首先根据圆柱的表面积公式:s=2πr2+2πrh,把数据代入公式求出圆柱的表面积,因为圆柱的底面半径是4厘米,所以圆柱容球时高为(4×2)厘米,因为球的表面积是圆柱表面积的三分之二,根据一个数乘分数的意义,即可求出球的表面积,据此解答.
解答 解:3.14×42×2+2×3.14×4×(4×2)
=3.14×16×2+25.12×8
=50.24×2+200.96
=100.48+200.96
=301.44(平方厘米),
301.44×$\frac{2}{3}$=200.96(平方厘米),
答:球的表面积是200.96平方厘米.
点评 此题主要考查圆柱的表面积公式、球的表面积公式的灵活运用,关键是熟记公式.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.按我国2009年公布的个人所得税征收标准,个人月收入超过2000元的部分,按一定比例收取税款.此项税款按表格中分级累计进行计算.
(1)陈洛的妈妈月收入3000元,应缴纳个人所得税多少元?
(2)陈洛的爸爸每月工资4000元,九月份其他收入1200元,陈洛的爸爸九月份税后的收入是多少元?
| 全月应纳所得税额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500~2000元的部分 | 10% |
| 超过2000~5000元的部分 | 15% |
| 超过5000~20000元的部分 | 20% |
| … | … |
(2)陈洛的爸爸每月工资4000元,九月份其他收入1200元,陈洛的爸爸九月份税后的收入是多少元?
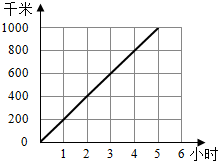 一列动车在高速铁路上行驶的时间和路程如图.看图填写:
一列动车在高速铁路上行驶的时间和路程如图.看图填写: