题目内容
如果a＜b＜0，那么
ab 0，a-b 0，a+b 2b．
| 5 | 6 |
分析：因为a＜b＜0，根据负负得正，可得ab＞0，则
ab＞0；
又因为a的绝对值等于b的绝对值，所以a-b的符号取负号，所以a-b＜0；
a与b都是负数，两个数相加取与加数相同的符号，所以a+b＜0，据此即可填空．
| 5 |
| 6 |
又因为a的绝对值等于b的绝对值，所以a-b的符号取负号，所以a-b＜0；
a与b都是负数，两个数相加取与加数相同的符号，所以a+b＜0，据此即可填空．
解答：解：因为a＜b＜0，根据负负得正，可得ab＞0，
则
ab＞0；
又因为a的绝对值等于b的绝对值，所以a-b的符号取负号，
所以a-b＜0；
a与b都是负数，两个数相加取与加数相同的符号，
所以a+b＜0，
故答案为：＞；＜；＜．
则
| 5 |
| 6 |
又因为a的绝对值等于b的绝对值，所以a-b的符号取负号，
所以a-b＜0；
a与b都是负数，两个数相加取与加数相同的符号，
所以a+b＜0，
故答案为：＞；＜；＜．
点评：此题主要考查有理数的运算中，运算符号的判断方法．
练习册系列答案
阅读快车系列答案
相关题目
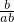一定小于
．
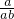ab________0，a-b________0，a+b________2b．