题目内容
15.新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有17人.分析 用韦恩图可以清晰的呈现各个集合之间的数量关系:设只参加合唱的有x人,那么只参加跳舞的人数为3x,由50人没有参加演奏,10人同时参加了跳舞和合唱但没有参加演奏,得到只参加合唱的和只参加跳舞的人数和为50-10=40,所以只参加合唱的有10人,那么只参加跳舞的人数为30人,又由“同时参加三种节目的人比只参加合唱的人少7人”,得到同时参加三项的有3人,所以参加了合唱的人中同时参加了演奏、合唱但没有参加跳舞的有:40-10-10-3=17人.
解答 解:只参加合唱的和只参加跳舞的人数和为:50-10=40(人),
所以只参加合唱的有10人,那么只参加跳舞的人数为30人,
所以参加了合唱的人中同时参加了演奏、合唱但没有参加跳舞的有:40-10-10-3=17(人),
答:同时参加了演奏、合唱但没有参加跳舞的有17人.
故答案为:17.
点评 解答此题关键是明确参加合唱的和只参加跳舞的人数和为40人.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.准确计算
| 9.9+9= | 48×12.5%= | 2.1-2.01= | 1-$\frac{3}{7}$+$\frac{4}{7}$= |
| 5÷$\frac{5}{9}$-$\frac{5}{9}$÷5= | 0.3+0.32= | $\frac{3}{8}$+0.75= | 64÷0.04= |
| 3.7×$\frac{6}{5}$+1.3÷$\frac{5}{6}$= | $\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+…+$\frac{1}{64}$= |
4.算式1.23+1.23+1.23+…+1.23的结果不可能是( )
| A. | 6.15 | B. | 12.3 | C. | 8.61 | D. | 13.43 |
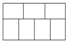 如图,用七个完全一样的小长方形正好拼成一个大长方形,如果大长方形的宽是14厘米,则大长方形的面积是336平方厘米.
如图,用七个完全一样的小长方形正好拼成一个大长方形,如果大长方形的宽是14厘米,则大长方形的面积是336平方厘米.