题目内容
下表框出的5个数的和是60,在表中移动这个粗线框,可以使每次框出的5个数的和各不相同.| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
(2)如果框出的5个数的和是140,应该怎样框?在表中画出来.
(3)你能框出和是250的5个数吗?为什么?
(4)一共可以框出多少个不同的和?
分析:(1)根据框出的5个数的和和中间的数的特点,可得出这五个数的和是中间数的5倍,据此即可解答.
(2)根据题意发现框出的5个数和是中间数的5倍的规律,即可得出框法,从而找到和是140的中间数是140÷5=28,据此即可框出;
(3)因为250÷5=50,即中间数应该是50,根据表格中50的位置,可得,框不出和是250的5个数.
(4)原来“十”字形框左右平移一共有8个,原来的“十”字形框上下平移一共有4个,一共就有8×4=32(个).
(2)根据题意发现框出的5个数和是中间数的5倍的规律,即可得出框法,从而找到和是140的中间数是140÷5=28,据此即可框出;
(3)因为250÷5=50,即中间数应该是50,根据表格中50的位置,可得,框不出和是250的5个数.
(4)原来“十”字形框左右平移一共有8个,原来的“十”字形框上下平移一共有4个,一共就有8×4=32(个).
解答:解:(1)2+11+12+13+22=60=12×5
3+12+13+14+23=65=13×5
4+13+14+15+24=14×5
所以可得:框出的5个数的和是中间数的5倍.
(2)根据规律框出的5个数的和是中间数的5倍可得:中间数是140÷5=28,其它四个数:28上面是18,下面是38,左边是27,右边是29,据此在表格中画出如下:
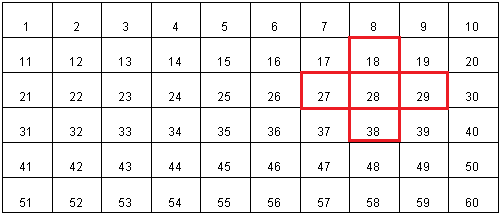
(3)根据规律框出的5个数的和是中间数的5倍可得:中间数是250÷5=50,因为50的右边没有数字;所以不能框出.
(4)8×3=24(个);
答:一共可以框出24个不同的和.
3+12+13+14+23=65=13×5
4+13+14+15+24=14×5
所以可得:框出的5个数的和是中间数的5倍.
(2)根据规律框出的5个数的和是中间数的5倍可得:中间数是140÷5=28,其它四个数:28上面是18,下面是38,左边是27,右边是29,据此在表格中画出如下:

(3)根据规律框出的5个数的和是中间数的5倍可得:中间数是250÷5=50,因为50的右边没有数字;所以不能框出.
(4)8×3=24(个);
答:一共可以框出24个不同的和.
点评:解答此题的关键是,根据所给的框法,及表中数的特点,即可找出它们之间的规律,再根据规律作答即可.

练习册系列答案
相关题目
 的长方形框去框下表中的数.
的长方形框去框下表中的数.


