题目内容
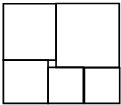 (2010?哈尔滨模拟)如图,长方形被分割成大小不等的6个正方形,已知中央的小正方形的面积为4平方厘米.长方形的面积是
(2010?哈尔滨模拟)如图,长方形被分割成大小不等的6个正方形,已知中央的小正方形的面积为4平方厘米.长方形的面积是572
572
平方厘米.分析:由中央小正方形面积为4平方厘米,可求出小正方形的边长为2厘米,设这6个正方形中最大的一个边长为x厘米,其余几个边长分别是x-2、x-4、x-6(单位厘米),根据长方形中几个正方形的排列情况,列方程求出最大正方形的边长,从而求得长方形长和宽,进而求出长方形的面积.
解答:解:因为小正方形面积为4平方厘米,所以小正方形的边长为2厘米,
设这6个正方形中最大的一个边长为x厘米,
因为图中最小正方形边长是1厘米,
所以其余的正方形边长分别为x-2,x-4,x-6,x-6,
x+x-2=2(x-6)+(x-4),
解这个方程得:x=14;
所以长方形的长为 x+x-2=26,宽为x+x-6=22,
长方形的面积为 26×22=572(平方厘米);
故答案为:572
设这6个正方形中最大的一个边长为x厘米,
因为图中最小正方形边长是1厘米,
所以其余的正方形边长分别为x-2,x-4,x-6,x-6,
x+x-2=2(x-6)+(x-4),
解这个方程得:x=14;
所以长方形的长为 x+x-2=26,宽为x+x-6=22,
长方形的面积为 26×22=572(平方厘米);
故答案为:572
点评:解决此题关键是理解图,找出正方形边长之间的关系,求出长方形的长和宽,进一步用长乘宽求得面积.

练习册系列答案
相关题目
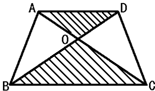 (2010?哈尔滨模拟)如图,已知梯形ABCD中AD=
(2010?哈尔滨模拟)如图,已知梯形ABCD中AD=