题目内容
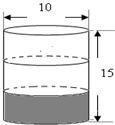 阴影部分表示所装水高度,圆柱内的水倒入( )内正好倒满.
阴影部分表示所装水高度,圆柱内的水倒入( )内正好倒满.分析:先利用圆柱的容积公式求出圆柱内水的体积,再利用圆锥的体积公式,分别计算出A、B、C选项中圆锥的容积即可进行选择.
解答:解:水的体积占圆柱容积的
是:15×π×(
)2÷3,
=15π×25÷3,
=125π,
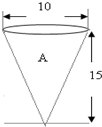
A:根据图形可知此圆锥与题干中的圆柱等底等高,所以它的容积等于圆柱的容积的
,是125π,
所以把圆柱内的沙子倒入圆锥中,正好倒满;
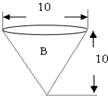
B:
×π×(
)2×10,
=
π×25×10,
=
π;
所以把圆柱内的沙子倒入此圆锥中不能倒满;
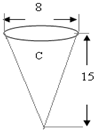
C:
×π×(
)2×15,
=
π×16×15,
=80π,
所以把圆柱内的水倒入此圆锥中能倒满,但还有剩余;
故选:A.
| 1 |
| 3 |
| 10 |
| 2 |
=15π×25÷3,
=125π,
A:根据图形可知此圆锥与题干中的圆柱等底等高,所以它的容积等于圆柱的容积的
| 1 |
| 3 |
所以把圆柱内的沙子倒入圆锥中,正好倒满;
B:
| 1 |
| 3 |
| 10 |
| 2 |
=
| 1 |
| 3 |
=
| 250 |
| 3 |
所以把圆柱内的沙子倒入此圆锥中不能倒满;
C:
| 1 |
| 3 |
| 8 |
| 2 |
=
| 1 |
| 3 |
=80π,
所以把圆柱内的水倒入此圆锥中能倒满,但还有剩余;
故选:A.
点评:此题也可以直接利用圆柱容积的
和与它等底等高的圆锥的容积相等,直接选择A.
| 1 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 小明喜欢:踢足球、上网、游泳、音乐、语文、数学;小英喜欢:数学、英语、音乐、陶艺、跳绳.用圆A、圆B分别表示小明、小英的爱好,如图所示,则图中阴影部分表示
小明喜欢:踢足球、上网、游泳、音乐、语文、数学;小英喜欢:数学、英语、音乐、陶艺、跳绳.用圆A、圆B分别表示小明、小英的爱好,如图所示,则图中阴影部分表示

 阴影部分表示所装水高度,圆柱内的水倒入内正好倒满.
阴影部分表示所装水高度,圆柱内的水倒入内正好倒满.