题目内容
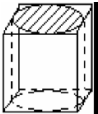 一个立方体的纸盒中,恰好能放入一个体积为6.28立方厘米的圆柱体,纸盒的容积是________立方厘米.(圆周率=3.14)
一个立方体的纸盒中,恰好能放入一个体积为6.28立方厘米的圆柱体,纸盒的容积是________立方厘米.(圆周率=3.14)
8
分析:根据题干分析可得,这个圆柱的底面直径和高都等于正方体的棱长,由此设这个正方体的棱长是x厘米,则圆柱的底面直径和高也是x厘米,由此根据圆柱的体积公式列出方程,即可求出x3的值,即得正方体纸盒的容积.
解答:设这个正方体的棱长是x厘米,则圆柱的底面直径和高也是x厘米,则:
3.14×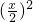 ×x=6.28,
×x=6.28,
3.14× ×x=6.28,
×x=6.28,
0.785x3=6.28,
x3=8,
答:这个纸盒的容积是8立方厘米.
故答案为:8.
点评:此题考查了正方体和圆柱的体积公式的灵活应用,解答此题的关键是正方体内最大的圆柱的特点.
分析:根据题干分析可得,这个圆柱的底面直径和高都等于正方体的棱长,由此设这个正方体的棱长是x厘米,则圆柱的底面直径和高也是x厘米,由此根据圆柱的体积公式列出方程,即可求出x3的值,即得正方体纸盒的容积.
解答:设这个正方体的棱长是x厘米,则圆柱的底面直径和高也是x厘米,则:
3.14×
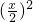 ×x=6.28,
×x=6.28,3.14×
 ×x=6.28,
×x=6.28,0.785x3=6.28,
x3=8,
答:这个纸盒的容积是8立方厘米.
故答案为:8.
点评:此题考查了正方体和圆柱的体积公式的灵活应用,解答此题的关键是正方体内最大的圆柱的特点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一个立方体的纸盒中,恰好能放入一个体积为6.28立方厘米的圆柱体,纸盒的容积是
一个立方体的纸盒中,恰好能放入一个体积为6.28立方厘米的圆柱体,纸盒的容积是