题目内容
【题目】某人走12千米路程,他行走的速度与所用时间的关系如下表:
速度(km/h) | 1 | 2 | 3 | 4 | 5 | 6 |
时间(h) | 12 | 6 | 4 | 3 | 2.4 | 2 |
(1)根据上表数据,在图一中找出各点,并顺次连结各点。
(2)如果以1.5千米/时的速度行进,大约需用( )小时才能走完。
(3)如果想用3小时走完,速度应达到( )千米/时。
(4)从图中你发现了什么?
【答案】(1)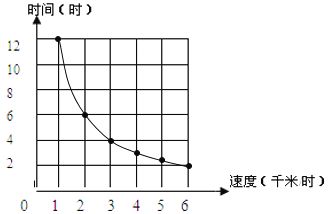 ;(2)8;(3)4;(4)路程不变,速度越快,用时越少。
;(2)8;(3)4;(4)路程不变,速度越快,用时越少。
【解析】
本题是正反比例的知识点的综合运用,也渗透一定的函数思想、数形结合的思想。
(1)画图时,首先要明确横轴、纵轴所表示的意义及单位长度所表示的量,找出各点依次连结。如图:

(2)由1.5米/时在纵轴上对应的点可知:大约需用8小时才能走完。
(3)由3小时在横轴上对应的点可知:速度应为4千米/时。
(4)由图上,我们可以发现:速度越快,所需时间越少;速度越慢,所需时间越多;对应的速度和时间的乘积相等;速度和时间是成反比例的量。

 阅读快车系列答案
阅读快车系列答案【题目】小学生数学报社组织小学数学奥林匹克竞赛,各位选手的决赛成绩(单位:分)如下表所示。
编号 | 成绩 | 编号 | 成绩 | 编号 | 成绩 | 编号 | 成绩 | 编号 | 成绩 | 编号 | 成绩 |
1 | 98 | 7 | 95 | 13 | 79 | 19 | 75 | 25 | 79 | 31 | 68 |
2 | 85 | 8 | 84 | 14 | 98 | 20 | 86 | 26 | 80 | 32 | 78 |
3 | 94 | 9 | 90 | 15 | 93 | 21 | 76 | 27 | 85 | 33 | 80 |
4 | 95 | 10 | 100 | 16 | 85 | 22 | 66 | 28 | 94 | 34 | 79 |
5 | 93 | 11 | 99 | 17 | 88 | 23 | 84 | 29 | 100 | 35 | 89 |
6 | 66 | 12 | 92 | 18 | 93 | 24 | 88 | 30 | 56 | 36 | 90 |
(1)请你将这次竞赛成绩整理后填入下表。
分数 | 100 | 90~99 | 80~89 | 70~79 | 60~69 | 60以下 |
人数 | (______) | (______) | (______) | (______) | (______) | (______) |
(2)(________)这一分数段的人数最多,(________)这一分数段的人数最少。
(3)按要求这次竞赛设置一等奖5人,二等奖10人,其余为三等奖。请你把分数重新分段。一等奖:(________)分;二等奖:(________)分;三等奖:(________)分以下。
【题目】磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | …… |
路程/千米 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | …… |
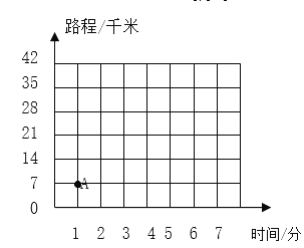
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗?
(3)根据图像判断,列车运行2分半钟时,行驶的路程是多少千米?行驶30千米大约需要几分钟?
【题目】某市有一项工程举行公开招标,有甲、乙、丙三家公司参加竞标。三家公司的竞标条件如下:
公司名称 | 单独完成工程所需天数 | 每天工资(万元) |
甲 | 10 | 5.6 |
乙 | 15 | 3.8 |
丙 | 30 | 1.7 |
(1)如果想尽快完工,应该选择哪两家公司合作?需要多少天完成?
(2)如果想尽量降低工资成本,应该选择哪两家公司合作?完工时要付工资多少元?