题目内容
5.如图是一个平行四边形,用经过D点的两条直线将这个图形分成面积相等的三部分.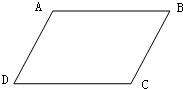
分析 D点是平行四边形的一个顶点,经过D点的两条直线将这个图形分成面积相等的三部分,则每一部分占平行四边形面积的$\frac{1}{3}$,所以可取两点E、F,使E、F是AB和BC边上的点,且满足BE=$\frac{1}{3}$AB,BF=$\frac{1}{3}$BC,那么 DE、DF将平行四边形ABCD分成面积相等的3部分.
解答 解:在AB、BC上各取点E、F,使BE=$\frac{1}{3}$AB,BF=$\frac{1}{3}$BC,
那么DE、DF将平行四边形ABCD分成面积相等的3部分.
点评 解答此题关键是明确:每一部分占平行四边形面积的$\frac{1}{3}$,在相邻的两边上各取$\frac{1}{3}$点,即把平行四边形的面积分成6等份,每一部分是2份,即占平行四边形面积的$\frac{1}{3}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.被除数扩大2倍,除数缩小2倍,商( )
| A. | 不变 | B. | 扩大4倍 | C. | 缩小4倍 |
15.把一段圆柱形的木料削成一个体积最大的圆锥,则这个圆锥的体积是削去部分的体积的( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 2倍 |