题目内容
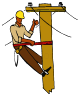
【题目】正方形操场四周栽了一圈树,每两棵树相隔5米.甲乙二人同时从一个角出发,向不同的方向走去(如图),甲的速度是乙的2倍,乙在拐了第一弯之后的第5棵树与甲相遇.操场四周一共栽了多少棵树?

【答案】60
【解析】
试题分析:由于甲速是乙速的2倍,所以乙在拐了第一弯时,甲正好拐了两个弯,即两个人开始同时沿着最上边走.乙走过了5棵树,也就是走过了5个间隔,所以甲走过了10个间隔,即正方形操场一边上的间隔数是10+5,则四周一共有(5+10)×4=60个间隔,根据植树问题中,围成一个封闭的图形植树时,植树棵数=间隔数,所以一共栽了60棵树.
解:根据题干分析可得,四周一共有间隔:(5+10)×4=60(个),
所以一共植树60棵.
答:操场四周一共栽了60棵树.

练习册系列答案
相关题目