题目内容
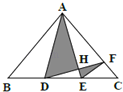
【题目】在△ABC中，BD=DE=EC，CF：AC=1：3．若△ADH的面积比△HEF的面积多24平方厘米，求三角形ABC 的面积是多少平方厘米？
【答案】108平方厘米
【解析】
试题分析：由题意可知：△ADH的面积比△HEF的面积多24平方厘米，则三角形ADE的面积比三角形FDE的面积多24平方厘米，又因三角形FDE和三角形FEC的面积相等，也就是说三角形AEC比三角形FEC的面积多24平方厘米，又因多出的24平方厘米，是三角形AEC的面积的
，所以三角形AEC的面积是36平方厘米，从而求得三角形ABC的面积．
解：△ADH的面积比△HEF的面积多24平方厘米，
则三角形ADE的面积比三角形FDE的面积多24平方厘米，
又因三角形FDE和三角形FEC的面积相等，
也就是说三角形AEC比三角形FEC的面积多24平方厘米，
又因多出的24平方厘米，是三角形AEC的面积的，
所以三角形AEC的面积是24÷=36平方厘米，
则三角形ABC的面积是36÷
=108（平方厘米），
答：三角形ABC的面积是108平方厘米．
练习册系列答案
相关题目
