题目内容
 一个长方体的长是30cm,宽14cm,高10cm,截成棱长为3cm的正方体.
一个长方体的长是30cm,宽14cm,高10cm,截成棱长为3cm的正方体.(1)最多能截成几个?
(2)求剩下“L”形的表面积.
分析:(1)要求取得尽可能多,就看沿着长方体木块长、宽、高分别切取多少个,即看30cm、14cm、10cm分别包含了多少个3cm;
(2)结合剩下的L形木块的表面积和切取的长方体的高是9cm、长是12cm、宽还是30cm,所以比原来减少的表面积仅仅是两个9×12的长方形的面的面积;然后用原来长方体的表面积减去这两个9×12的长方形的面的面积即是剩下的L形木块的表面积.
(2)结合剩下的L形木块的表面积和切取的长方体的高是9cm、长是12cm、宽还是30cm,所以比原来减少的表面积仅仅是两个9×12的长方形的面的面积;然后用原来长方体的表面积减去这两个9×12的长方形的面的面积即是剩下的L形木块的表面积.
解答:解:(1)(30÷3)×(14÷3)×(10÷3);
≈10×4×3,
=120(块);
答:被切掉的小正方体有120块.
(2)14÷3≈4(个),4×3=12(厘米);
10÷3≈3(个),3×3=9(厘米);
(30×14+30×10+14×10)×2-9×12×2,
=(420+300+140)×2-216,
=1720-216,
=1504(平方厘米);
答:剩下的L形木块的表面积是1504平方厘米.
≈10×4×3,
=120(块);
答:被切掉的小正方体有120块.
(2)14÷3≈4(个),4×3=12(厘米);
10÷3≈3(个),3×3=9(厘米);
(30×14+30×10+14×10)×2-9×12×2,
=(420+300+140)×2-216,
=1720-216,
=1504(平方厘米);
答:剩下的L形木块的表面积是1504平方厘米.
点评:(1)本题因为长方体木块的长、宽、高不全是3的倍数,所以求被切掉的小正方体有多少块,不能用长方体的体积除以一个小正方体的体积;
(2)不要单独的求剩下的L形木块的表面积,那样计算比较麻烦,要认真分析增加的和减少的面的面积之间的关系.
(2)不要单独的求剩下的L形木块的表面积,那样计算比较麻烦,要认真分析增加的和减少的面的面积之间的关系.

练习册系列答案
相关题目
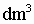 ,长6dm,宽5dm,高是( )dm.
,长6dm,宽5dm,高是( )dm.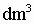 ,长6dm,宽5dm,高是( )dm.
,长6dm,宽5dm,高是( )dm.