题目内容
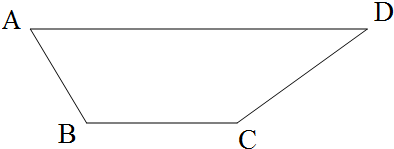
3. 如图,长方形ABCD中,AB=5厘米,BC=3厘米.把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,使点C落在点C′处.则A点和C点所经过的路程之比为5:3.
如图,长方形ABCD中,AB=5厘米,BC=3厘米.把长方形ABCD绕顶点B顺时针转动,使点A落在点A′处,使点C落在点C′处.则A点和C点所经过的路程之比为5:3.
分析 由题意可知:从点A落在点A′出A点经过的路程是以AB为半径的$\frac{1}{4}$圆周长,点C落在点C′处,C点所经过的路程是以BC为半径的$\frac{1}{4}$圆周长,据此利用圆的周长公式C=2πr即可求解.
解答 解:(π×5×2×$\frac{1}{4}$):(π×3×2×$\frac{1}{4}$)=5:3
答:A点和C点所经过的路程之比为5:3.
故答案为:5:3.
点评 此题主要考查圆的周长公式的灵活应用,关键是弄清楚它们所行路程是一个什么样的图形.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.课桌高约8( )
| A. | 米 | B. | 分米 | C. | 厘米 |
8.已知三个数为2、3、4,再写出一个数,使这四个数能组成一个比例式,这个数不能是( )
| A. | $\frac{3}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
13.下列各数中,与1最接近的数是( )
| A. | 2.81 | B. | $\frac{14}{5}$ | C. | 2.79 | D. | 2$\frac{9}{11}$ |
 右面是某小学六年级同学参加课外兴趣小组的分布情况统计图.
右面是某小学六年级同学参加课外兴趣小组的分布情况统计图.