题目内容
某工厂有若干个工人,其中
是党员,
是团员(n为正整数),其余88人是群众,则此工厂共有
| 1 |
| 5 |
| n |
| 3 |
660
660
人.分析:“
是团员(n为正整数)”这个条件告诉我们:n可以为1或2,也就是
是
或
;由题意可得出数量关系:
总人数-党员人数-团员人数=群众人数,可据此关系分两种情况列方程解答.
| n |
| 3 |
| n |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
总人数-党员人数-团员人数=群众人数,可据此关系分两种情况列方程解答.
解答:解:(1)当n=1时,
设此工厂共有x人,由题意得:
x-
x-
x=88
x=88
x=
;
(2)当n=2时,
设此工厂共有x人,由题意得:
x-
x-
x=88
x=88
x=660;
由于总人数是正整数,所以第一种情况不存在,应舍去;第二种情况符合题意;
故答案为660.
设此工厂共有x人,由题意得:
x-
| 1 |
| 5 |
| 1 |
| 3 |
| 7 |
| 15 |
x=
| 1320 |
| 7 |
(2)当n=2时,
设此工厂共有x人,由题意得:
x-
| 1 |
| 5 |
| 2 |
| 3 |
| 2 |
| 15 |
x=660;
由于总人数是正整数,所以第一种情况不存在,应舍去;第二种情况符合题意;
故答案为660.
点评:此题是复杂的分数应用题,且有两种情况的存在,故要对两种情况都要分析解答后再作判断.

练习册系列答案
相关题目
 是党员,
是党员,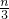 是团员(n为正整数),其余88人是群众,则此工厂共有________人.
是团员(n为正整数),其余88人是群众,则此工厂共有________人.