题目内容
 有一个底角为60°腰长为15cm,下底长是上底长2倍的等腰梯形,把两腰平均分成30份,然后把对应等分点连起来,这些线段总长是多少cm?
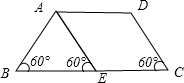
有一个底角为60°腰长为15cm,下底长是上底长2倍的等腰梯形,把两腰平均分成30份,然后把对应等分点连起来,这些线段总长是多少cm?分析:由题意及图,我们可以设想做一条辅助线,取下底BC中点E,连接AE,则BE=AD=
BC=AB,又因为∠ABC=60度,则△ABE是等边三角形;且四边形AECD是平行四边形且是菱形. 在梯形ABCD的两腰上,分成30等分,连接两腰的对应等分点,在平行四边形ABCE内,对应等分点连起来的这些(包括上下底)线段总长是:(30+1)×15=31×15 (cm);这些对应等分点连起来的这些线段,处于△ABE内的部分总长是:[
+
+
+…+
+
+
]×15 (cm).那么,把这两部分相加的和即为所求.如图:
| 1 |
| 2 |
| 30 |
| 30 |
| 29 |
| 30 |
| 28 |
| 30 |
| 3 |
| 30 |
| 2 |
| 30 |
| 1 |
| 30 |

解答:解:如图,
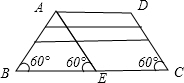
取下底BC中点E,连接AE,由题意则BE=AD=BC÷2=AB=15cm,又因为∠ABC=60°,
则△ABE是等边三角形;且四边形AECD是平行四边形且是菱形.
在梯形ABCD的两腰上,分成30等分,连接两腰的对应等分点,在平行四边形ABCE内,对应等分点连起来的这些(包括上下底)线段总长是:
(30+1)×15=31×15(cm);
处于△ABE内的这些对应等分点连起来的这些线段总长是:
[
+
+
+…+
+
+
]×15 (cm).,
其中,(30/30)×15 cm是△ABE的底边,
则,对应等分点连起来形成的这些线段总长是:
31×15+[
+
+
+…+
+
+
]×15
=31×15+
×15
=465+
×15
=465+
=697.5 (cm)
答:这些线段总长697.5cm.

取下底BC中点E,连接AE,由题意则BE=AD=BC÷2=AB=15cm,又因为∠ABC=60°,
则△ABE是等边三角形;且四边形AECD是平行四边形且是菱形.
在梯形ABCD的两腰上,分成30等分,连接两腰的对应等分点,在平行四边形ABCE内,对应等分点连起来的这些(包括上下底)线段总长是:
(30+1)×15=31×15(cm);
处于△ABE内的这些对应等分点连起来的这些线段总长是:
[
| 30 |
| 30 |
| 29 |
| 30 |
| 28 |
| 30 |
| 3 |
| 30 |
| 2 |
| 30 |
| 1 |
| 30 |
其中,(30/30)×15 cm是△ABE的底边,
则,对应等分点连起来形成的这些线段总长是:
31×15+[
| 30 |
| 30 |
| 29 |
| 30 |
| 28 |
| 30 |
| 3 |
| 30 |
| 2 |
| 30 |
| 1 |
| 30 |
=31×15+
| 30+29+28+…+3+2+1 |
| 30 |
=465+
| (1+30)×30÷2 |
| 30 |
=465+
| 465 |
| 2 |
=697.5 (cm)
答:这些线段总长697.5cm.
点评:本题是一个难度较高的等差数列应用题,综合考查了等差数列求和,等腰梯形、等边三角形的性质等知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目