题目内容
(2007?武汉)有三种型号的钢板A、B、C分别由3、3、4个1×1的小正方形组成,现有A型钢板7块,需购进B、C两种型号的钢板若干块,不重叠、无缝隙地拼成5×5的正方形钢板2块,已知B型钢每块500元,C型钢每块400元,请考虑B、C两种型号的钢板各购多少块,才能使所花的钱最少?计算出最省钱的方案,并画出设计图.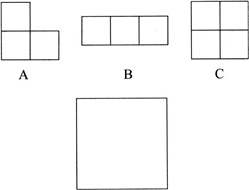

分析:要花钱最少,那么7块A全部用上;一共需要小正方形5×5×2=50;现在有了7×3=21个,还需要29个;设B型X块,C型Y块,则:3X+4Y=29;根据X、Y都是整数讨论出它们的取值,然后根据它们的单价,找出最省钱的方案;再根据A、B、C三种的块数,拼出两个5×5的正方形即可求解.
解答:解:5×5×2=50,
50-3×7=29
设B型X块,C型Y块,则:
3X+4Y=29,利用穷举法选取X,Y都是整数的情况,一共是2种:
X=7,Y=2;
或者:X=3,Y=5;
第一种需要:
7×500+2×400=4300(元),
第二种需要:
3×500+5×400=3500(元).
答:需要B型买3块,C型买5块,花钱最少为3500元.
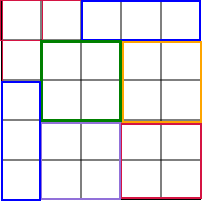
如下图:第一块钢板用6块A,1块B和1块C;
第二块钢板用1块A,2块B和4块C.

50-3×7=29
设B型X块,C型Y块,则:
3X+4Y=29,利用穷举法选取X,Y都是整数的情况,一共是2种:
X=7,Y=2;
或者:X=3,Y=5;
第一种需要:
7×500+2×400=4300(元),
第二种需要:
3×500+5×400=3500(元).
答:需要B型买3块,C型买5块,花钱最少为3500元.
如下图:第一块钢板用6块A,1块B和1块C;
第二块钢板用1块A,2块B和4块C.


点评:本题关键是根据需要的小正方形的个数,找出等量关系,讨论出B、C的块数,再画图求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目