Question

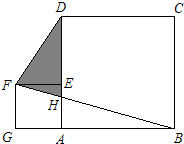ABCD与AEFG均为正方形，三角形ABH的面积为6平方厘米，图中阴影部分的面积是多少？

Answer 1

分析：根据梯形面积公式和三角形面积公式可得：梯形GFDA的面积=三角形GBF的面积，都减去公共部分AHFG的面积，可得图中阴影部分的面积=三角形ABH的面积．

解答：解：梯形GFDA的面积=（GF+AD）×AG÷2，
三角形GBF的面积=（AG+AB）×GF÷2，
因为ABCD与AEFG均为正方形，
所以（GF+AD）×AG÷2=（AG+AB）×GF÷2，
则梯形GFDA的面积=三角形GBF的面积，
则阴影部分的面积=三角形ABH的面积=6平方厘米．
答：图中阴影部分的面积是6平方厘米．

点评：本题的关键是根据正方形的边长相等，由梯形面积公式和三角形面积公式得到：梯形GFDA的面积=三角形GBF的面积．