题目内容
利用半径为4厘米的圆形纸片剪一个面积最大的正方形，此正方形的面积为________平方厘米．
32
分析：根据题意，连接正方形的两个对角线，则两个对角线成的夹角为90度，那正方形的面积就是由一条对角线分成的两个三角形的面积，再根据三角形的面积公式，解答即可．
解答：如图：
正方形ACBD的面积就是三角形ACD的面积和三角形CBD的面积和，
三角形ACD的面积是：
×DC×OA=×（4×2）×OA=4OA，
三角形CBD的面积是：×DC×OB=×（4×2）×OB=4OB，
正方形ABCD的面积是：4OA+4OB=4（OA+OB）=4×CD=4×4×2=32（平方厘米），
答：这个正方形的面积是32平方厘米，
故答案为：32．
点评：解答此题的关键是，根据题意，将正方形分成两个三角形，利用三角形的面积公式，解答即可．
分析：根据题意，连接正方形的两个对角线，则两个对角线成的夹角为90度，那正方形的面积就是由一条对角线分成的两个三角形的面积，再根据三角形的面积公式，解答即可．
解答：如图：
正方形ACBD的面积就是三角形ACD的面积和三角形CBD的面积和，
三角形ACD的面积是：
×DC×OA=×（4×2）×OA=4OA，三角形CBD的面积是：
×DC×OB=×（4×2）×OB=4OB，正方形ABCD的面积是：4OA+4OB=4（OA+OB）=4×CD=4×4×2=32（平方厘米），
答：这个正方形的面积是32平方厘米，
故答案为：32．
点评：解答此题的关键是，根据题意，将正方形分成两个三角形，利用三角形的面积公式，解答即可．
练习册系列答案
相关题目
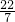、π、314%、这三个数中，最大是________，最小的是________．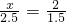
．
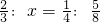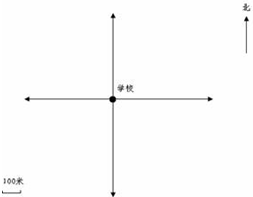根据下面的描述，在下图上标出少年宫和书店的位置．