题目内容
(1) x+
x+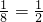
(2)X:8= :
: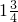
(3)85×0.75+4785÷15
(4)4×17×125×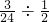
(5) ÷〔
÷〔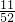 ÷
÷ ×(4.3-1.8)〕÷26
×(4.3-1.8)〕÷26
(6)〔1-( +
+ )〕÷
)〕÷
(7)n!表示从1到n的n个连续自然数的乘积,例如 10!=10×9×8×…×2×1请计算:1!+4!+5!
解:(1) x+
x+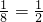 ,
,
 x+
x+ -
- =
= -
- ,
,
 x=
x= ,
,
 x×
x× =
= ×
× ,
,
x= ;
;
(2)X:8= :
: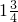 ,
,
1 X=8×
X=8× ,
,
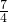 X=2,
X=2,
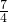 X×
X× =2×
=2× ,
,
X=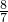 ;
;
(3)85×0.75+4785÷15,
=63.75+319,
=382.75;
(4)4×17×125×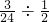 ,
,
=4×17×125× ×2,
×2,
=2125;
(5) ÷〔
÷〔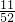 ÷
÷ ×(4.3-1.8)〕÷26,
×(4.3-1.8)〕÷26,
= ÷[
÷[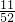 ×
×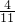 ×2.5]÷26,
×2.5]÷26,
= ÷[
÷[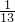 ×
× ]÷26,
]÷26,
= ÷
÷ ÷26,
÷26,
= ×
× ×
× ,
,
=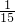 ;
;
(6)〔1-( +
+ )〕÷
)〕÷ ,
,
=[1- ]×3,
]×3,
= ×3,
×3,
=1;
(7)1!+4!+5!,
=1+1×2×3×4+1×2×3×4×5,
=1+24+120,
=145.
分析:(1)根据等式的性质,两边同减去 ,再同乘
,再同乘 即可;
即可;
(2)先根据比例的性质改写成1 X=8×
X=8× ,再根据等式的性质,两边同乘
,再根据等式的性质,两边同乘 即可;
即可;
(3)按运算顺序计算,先算乘法和除法,再算加法;
(4)把除法改为乘法,运用乘法交换律与结合律简算;
(5)先算小括号内的减法,原式变为 ÷[
÷[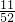 ×
×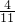 ×2.5]÷26,再算出中括号内的结果,然后把除法改为乘法,依次计算即可;
×2.5]÷26,再算出中括号内的结果,然后把除法改为乘法,依次计算即可;
(6)先算小括号内的,再算中括号内的,最后算括号外的;
(7)根据特例,列出算式,计算即可.
点评:此题考查了解方程以及四则混合运算,解方程时运用等式的性质,在做四则混合运算题时,注意运算顺序与运算技巧.
 x+
x+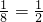 ,
, x+
x+ -
- =
= -
- ,
, x=
x= ,
, x×
x× =
= ×
× ,
,x=
 ;
;(2)X:8=
 :
: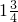 ,
,1
 X=8×
X=8× ,
,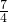 X=2,
X=2,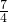 X×
X× =2×
=2× ,
,X=
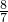 ;
;(3)85×0.75+4785÷15,
=63.75+319,
=382.75;
(4)4×17×125×
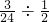 ,
,=4×17×125×
 ×2,
×2,=2125;
(5)
 ÷〔
÷〔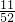 ÷
÷ ×(4.3-1.8)〕÷26,
×(4.3-1.8)〕÷26,=
 ÷[
÷[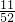 ×
×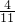 ×2.5]÷26,
×2.5]÷26,=
 ÷[
÷[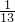 ×
× ]÷26,
]÷26,=
 ÷
÷ ÷26,
÷26,=
 ×
× ×
× ,
,=
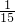 ;
;(6)〔1-(
 +
+ )〕÷
)〕÷ ,
,=[1-
 ]×3,
]×3,=
 ×3,
×3,=1;
(7)1!+4!+5!,
=1+1×2×3×4+1×2×3×4×5,
=1+24+120,
=145.
分析:(1)根据等式的性质,两边同减去
 ,再同乘
,再同乘 即可;
即可;(2)先根据比例的性质改写成1
 X=8×
X=8× ,再根据等式的性质,两边同乘
,再根据等式的性质,两边同乘 即可;
即可;(3)按运算顺序计算,先算乘法和除法,再算加法;
(4)把除法改为乘法,运用乘法交换律与结合律简算;
(5)先算小括号内的减法,原式变为
 ÷[
÷[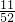 ×
×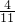 ×2.5]÷26,再算出中括号内的结果,然后把除法改为乘法,依次计算即可;
×2.5]÷26,再算出中括号内的结果,然后把除法改为乘法,依次计算即可;(6)先算小括号内的,再算中括号内的,最后算括号外的;
(7)根据特例,列出算式,计算即可.
点评:此题考查了解方程以及四则混合运算,解方程时运用等式的性质,在做四则混合运算题时,注意运算顺序与运算技巧.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 :3.5=1
:3.5=1 :x
:x 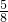 =2
=2 .
. x=20 (3)
x=20 (3)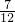 .
.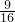 ÷
÷ x=4.
x=4.