题目内容
长方形ABCD被虚线分割成4个面积相等的部分(如下图,单位:厘米).试求线段BE的长度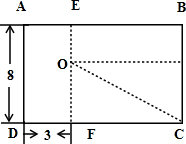
解:设FO=x厘米,CF=y厘米,
因为4个面积相等,
所以CF×FO=3×8×2=48(平方厘米),
即xy=48
EO×EB=3×8=24(平方厘米)
即(8-x)×y=3×8,
8y-xy=24,
8y=24+xy,
8y=24+48,
8y=72,
y=9,
即BE=9厘米;
答:线段BE的长是9厘米.
分析:如图,设FO=x厘米,CF=y厘米,根据长方形的面积公式S=ab,分别用x与y的式子表示出长方形OPCF的面积长方形EBPO的面积,应用代换的方法,解方程即可.
点评:关键是根据题意灵活利用长方形的面积公式及代换的方法解决问题.
因为4个面积相等,
所以CF×FO=3×8×2=48(平方厘米),
即xy=48
EO×EB=3×8=24(平方厘米)
即(8-x)×y=3×8,
8y-xy=24,
8y=24+xy,
8y=24+48,
8y=72,
y=9,
即BE=9厘米;
答:线段BE的长是9厘米.
分析:如图,设FO=x厘米,CF=y厘米,根据长方形的面积公式S=ab,分别用x与y的式子表示出长方形OPCF的面积长方形EBPO的面积,应用代换的方法,解方程即可.
点评:关键是根据题意灵活利用长方形的面积公式及代换的方法解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
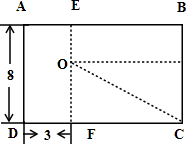
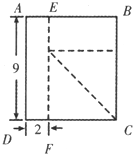 长方形ABCD被虚线分割成4个面积相等的部分(如图,单位:厘米).试求线段BE的长度.
长方形ABCD被虚线分割成4个面积相等的部分(如图,单位:厘米).试求线段BE的长度.