题目内容
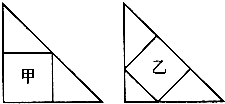
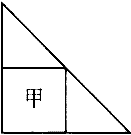
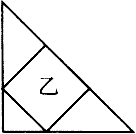
下图是两个完全相同的等腰直角三角形,甲和乙分别是等腰直角三角形的两种不同的内接正方形,则图中甲与乙的面积比是

9:8
9:8
.
分析:连接甲正方形的对角线,可知道正方形里的每个小三角形是等腰三角形的四分一,所以正方形甲的面积为等腰三角形的
;连接乙正方形的对角线,可知正方形的边长是对角线长的
,可以求出乙的面积是等腰三角形的
,所以甲与乙的面积比,是9:8.
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 9 |
解答:解:见下图:
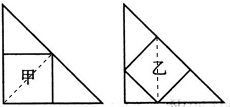
正方形甲的面积为等腰三角形的
;
正方形乙的面积为等腰三角形的
;
所以甲与乙的面积比是:
:
=9:8.
故答案为:9:8.

正方形甲的面积为等腰三角形的
| 1 |
| 2 |
正方形乙的面积为等腰三角形的
| 4 |
| 9 |
所以甲与乙的面积比是:
| 1 |
| 2 |
| 4 |
| 9 |
故答案为:9:8.
点评:解答此题关键是根据内接三角形的特征,先分别求出正方形甲的面积和正方形乙的面积占等腰三角形的几分之几,进而得解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2010?宜良县模拟)下图是两个完全相同的长方形,甲阴影部分的面积( )乙阴影部分的面积.
(2010?宜良县模拟)下图是两个完全相同的长方形,甲阴影部分的面积( )乙阴影部分的面积.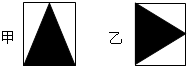 下图是两个完全相同的长方形,甲阴影部分的面积乙阴影部分的面积.
下图是两个完全相同的长方形,甲阴影部分的面积乙阴影部分的面积.