题目内容
(2011?长沙)用1根铁丝分别围成长方形、正方形和圆形,则围成的( )面积最大.
分析:根据题意可设铁丝的长为12.56米,根据正方形、长方形、圆形的周长公式分别计算出它们的边长、半径,然后再利用它们的面积公式分别计算出各自的面积,比较即可得到答案.
解答:解:设铁丝的长为12.56米,
正方形的边长是:12.56÷4=3.14(米),
正方形的面积是:3.14×3.14=9.8596(平方米);
长方形的长和宽的和是:12.56÷2=6.28(米),
长和宽越接近面积越大,长可为3.15米,宽为3.13米,
长方形的面积是:3.15×3.13=9.8595(平方米);
圆的半径是:12.56÷2÷3.14=2(米),
圆的面积是:2×2×3.14=12.56(平方米);
9.8595<9.8596<12.56;
所以围成的圆的面积最大.
故选:C.
正方形的边长是:12.56÷4=3.14(米),
正方形的面积是:3.14×3.14=9.8596(平方米);
长方形的长和宽的和是:12.56÷2=6.28(米),
长和宽越接近面积越大,长可为3.15米,宽为3.13米,
长方形的面积是:3.15×3.13=9.8595(平方米);
圆的半径是:12.56÷2÷3.14=2(米),
圆的面积是:2×2×3.14=12.56(平方米);
9.8595<9.8596<12.56;
所以围成的圆的面积最大.
故选:C.
点评:此题主要考查的是:在周长相等的所有图形中,围成的圆的面积最大.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,从正面看到
,从正面看到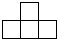 ,从上面看到( )
,从上面看到( )