题目内容
在黑板上从1开始，写出一组相继的自然数，然后擦去一个数，其余数的平均值为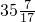
．问擦去的数是________．
7
分析：设n个数，因为其余数的平均值为35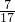
，所以n-1是17的倍数，确定n个数的取值范围，计算求解．
解答：设n个数擦去的是x，因为其余数的平均值为35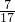，所以n-1是17的倍数，
即17个，34个，51个，68个，85个等，显然只有68个时所得平均数与35相差无几，
因为n=69，则1+2+…+69=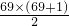
=2415，
那么n-1=68，则其他数的和是68×35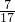=2408，
因为2415-2408=7，
所以擦去的数是7．
故答案为：7．
点评：本题考查了平均数的综合运用，正确运用分类讨论的思想是解答本题的关键．
分析：设n个数，因为其余数的平均值为35
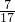，所以n-1是17的倍数，确定n个数的取值范围，计算求解．解答：设n个数擦去的是x，因为其余数的平均值为35
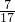，所以n-1是17的倍数，即17个，34个，51个，68个，85个等，显然只有68个时所得平均数与35相差无几，
因为n=69，则1+2+…+69=
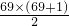=2415，那么n-1=68，则其他数的和是68×35
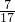=2408，因为2415-2408=7，
所以擦去的数是7．
故答案为：7．
点评：本题考查了平均数的综合运用，正确运用分类讨论的思想是解答本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目