题目内容
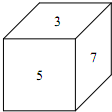如图，一个正方体的木块，六个面上分别写着数，相对面上两个数的和等于16，按照如图的位置摆好（上面是3，正面是5，右面是7），先顺时针方向从左向右翻转2011次，再由前向后翻转2012次，这时，这个木块正面的数是多少？
解：从左向右翻转，只有上下、左右四个面上的数字变化，前面和后面上的数字都不变化，从左向右翻转2011次后前面上的数字仍是5；
2012÷4=503；
2012是4的倍数，前向后翻转2012次，各个面上的数字都不变化，这个木块正面的数还是5．
答：这个木块正面的数是5．
分析：这个正方体按照同一个方向转4次各个面上的数字不变；先顺时针方向从左到右旋转2011次，正面和后面的数字不变；再从前向后翻转2012次，2012是4的倍数，各个面上的数字都不变，所以正面上的数字还是5．
点评：本题关键是找出翻转后数字变化的规律，再根据规律求解．
2012÷4=503；
2012是4的倍数，前向后翻转2012次，各个面上的数字都不变化，这个木块正面的数还是5．
答：这个木块正面的数是5．
分析：这个正方体按照同一个方向转4次各个面上的数字不变；先顺时针方向从左到右旋转2011次，正面和后面的数字不变；再从前向后翻转2012次，2012是4的倍数，各个面上的数字都不变，所以正面上的数字还是5．
点评：本题关键是找出翻转后数字变化的规律，再根据规律求解．
练习册系列答案
阅读快车系列答案
相关题目
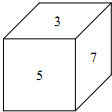如图，一个正方体的木块，六个面上分别写着数，相对面上两个数的和等于16，按照如图的位置摆好（上面是3，正面是5，右面是7），先顺时针方向从左向右翻转2011次，再由前向后翻转2012次，这时，这个木块正面的数是多少？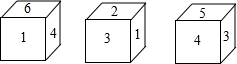
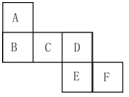如图是一个正方体的展开图，则A的对面是
如图是一个正方体的表面展开图．把它再折回成正方体，以下4个描述中，哪些情况是正确的？把正确描述的编号填在括号中．正确的描述有