题目内容
 如图,“○”中所填的数等于与之相连的三个“△”中的数的平均数,“□”中所填的数等于与之相连的三个“○”中的数的平均数.现将9,18,27,36,45分别填入五个“△”中,则“□”中的数的最大值等于
如图,“○”中所填的数等于与之相连的三个“△”中的数的平均数,“□”中所填的数等于与之相连的三个“○”中的数的平均数.现将9,18,27,36,45分别填入五个“△”中,则“□”中的数的最大值等于32
32
.用计算器找出最大的积.
(1)用1,2,3,4,5组成一个三位数和一个两位数,这两个数最大的乘积是
22412
22412
.(2)用0,2,4,5,6组成一个三位数和一个两位数,这两个数最大的乘积是
33480
33480
.分析:(1)要使三角中的数尽可能大,就要使三个方框中的三个数的和尽可能大;为了便于说明,不妨设五个△中的数依次为a、b、c、d、e,三个○中的数依次为x、y、z,□中的数为A,则有:x=
(a+b+c),y=
(b+c+d),z=
(c+d+e),于是
3x=a+b+c,3y=b+c+d,3z=c+d+e;即三个○里的数的3倍之和=a+b+b+c+c+c+d+d+e,中间△中c算了3次,两端△中的a、e各算1次,其余两个数各算2次,应将最大数放在中间△内,把最小和次小的数填在两端△内,剩下的两个数放在剩下的△内;进而解答即可;
(2)据乘法意义及乘法算式的性质可知,乘法算式中的因数越大,积就越大;根据数位知识可知,一个数的高位上数字越大,其值就越大.又因为现在各个数的和一定的情况下,两个因数越接近,它们的乘积就越大,由此可知,要想两位数最大就要把最大的数字放在十位,要把第二大的数字放在三位数的百位表示,然后再把第三大的数字放在三位数的十位,最后把剩下的两个数分别放在三位数与两位两位数的个位,据此得到三位数和两位数;要想使乘积最小,思路正好与乘积最大的相反,由此得到最小的两个.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
3x=a+b+c,3y=b+c+d,3z=c+d+e;即三个○里的数的3倍之和=a+b+b+c+c+c+d+d+e,中间△中c算了3次,两端△中的a、e各算1次,其余两个数各算2次,应将最大数放在中间△内,把最小和次小的数填在两端△内,剩下的两个数放在剩下的△内;进而解答即可;
(2)据乘法意义及乘法算式的性质可知,乘法算式中的因数越大,积就越大;根据数位知识可知,一个数的高位上数字越大,其值就越大.又因为现在各个数的和一定的情况下,两个因数越接近,它们的乘积就越大,由此可知,要想两位数最大就要把最大的数字放在十位,要把第二大的数字放在三位数的百位表示,然后再把第三大的数字放在三位数的十位,最后把剩下的两个数分别放在三位数与两位两位数的个位,据此得到三位数和两位数;要想使乘积最小,思路正好与乘积最大的相反,由此得到最小的两个.
解答:解:(1)由分析可知:即三个○里的数的3倍之和=a+b+b+c+c+c+d+d+e,中间△中c算了3次,两端△中的a、e各算1次,其余两个数各算2次,应将最大数放在中间○内,把最小和次小的数填在两端△内,剩下的两个数放在剩下的△内;
即:3x+3y+3z=45×3+36×2+27×2+18+9,
3(x+y+z)=288,
x+y+z=288÷3,
x+y+z=96;
A=(x+y+z)÷3=96÷3=32;
(2)用1,2,3,4,5这五个数字组成一个三位数和一个两位数,用计算器找出这两个数的最大乘积:431×52=22412.
(3)用0,2,4,5,6这五个数字组成一个三位数和一个两位数,用计算器找出这两个数的最大乘积:540×62=33480.
故答案为:32,22412,33480.
即:3x+3y+3z=45×3+36×2+27×2+18+9,
3(x+y+z)=288,
x+y+z=288÷3,
x+y+z=96;
A=(x+y+z)÷3=96÷3=32;
(2)用1,2,3,4,5这五个数字组成一个三位数和一个两位数,用计算器找出这两个数的最大乘积:431×52=22412.
(3)用0,2,4,5,6这五个数字组成一个三位数和一个两位数,用计算器找出这两个数的最大乘积:540×62=33480.
故答案为:32,22412,33480.
点评:解答此题的关键应结合平均数的计算方法和本题中数的关系进行解答即可;注意,在三位数与两位数中的同位数上,大数应优先两位数.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
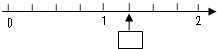 (2008?宝应县)如图方框中所填的分数应该是( )
(2008?宝应县)如图方框中所填的分数应该是( )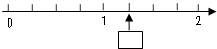 如图方框中所填的分数应该是
如图方框中所填的分数应该是