题目内容
2.任意一个三角形中至少有2个锐角.三角形的内角和是180度.分析 根据三角形的内角和等于180°,假设任意一个三角形至少有1个锐角,则另外两个内角的度数和就会等于或大于180度,这与三角形的内角和是180度是相违背的,故假设不成立,从而可以判断出任意一个三角形至少有2个锐角.据此判断.
解答 解:三角形的内角和是180度.
假设任意一个三角形至少有1个锐角,
则另外两个内角的度数和就会等于或大于180度,
那么三角形的内角和就大于180度,
这与三角形的内角和是180度是相违背的,
所以任意一个三角形至少有2个锐角.
故答案为:2、180.
点评 此题主要考查三角形的内角和等于180度,利用假设法即可求解.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 0是最小的数 | B. | 负数不一定比正数大 | ||
| C. | 在直线上表示数时,-7在-4的左边 |
10.560480000中的“6”表示什么?( )
| A. | 6个千万 | B. | 6个亿 | C. | 6个十亿 |

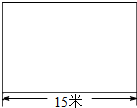 李庄小学有一块长方形草坪,长15米.在修建校园时,草坪的长增加了3米,这样草坪的面积就增加了30平方米.原来草坪的面积是多少平方米?(先在图中画出增加的部分,再解答)
李庄小学有一块长方形草坪,长15米.在修建校园时,草坪的长增加了3米,这样草坪的面积就增加了30平方米.原来草坪的面积是多少平方米?(先在图中画出增加的部分,再解答)