题目内容

已知a：b=2：3，b：c=1：2，并且以a+b+c=32，那么a=________．

$\text{[math]}$
分析：由根据比的性质b：c=1：2=（1×3）：（2×3），再由a：b=2：3，可知a：b：c=2：3：6，a取2份，b取3份，c取6份，一共11份，则a就占a、b、c总和的 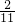$\text{[math]}$ = $\text{[math]}$ ，再用32× 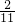$\text{[math]}$ 即可解决．
解答：b：c=1：2=（1×3）：（2×3）=3：6，再由a：b=2：3，
所以a：b：c=2：3：6，
故a就占a、b、c总和的 $\text{[math]}$ = $\text{[math]}$ ，
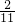a=32× $\text{[math]}$ = $\text{[math]}$ ，
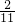故答案为： $\text{[math]}$ ．
点评：解答此题关键是把两个比中共同的量b换算成相同的份数，继而求出a：b：c的值．