题目内容
例题4解答下面两道应用题,并比较它们思路上的异同.
(1)小明读一本书,一天后已读页数和未读页数的比是1:5,第二天比第一天多读6页,这时已读页数和未读页数的比是3:5,这本书有几页?
(2)某班体育达标人数是没达标人数的 ,如果又有2名达标,达标人数是没达标人数的
,如果又有2名达标,达标人数是没达标人数的 ,求全班的人数.
,求全班的人数.
解(1)以总页数为单位“1”,一天后读过的页数是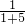 ,两天后是
,两天后是 ,第二天读的页数是(
,第二天读的页数是(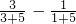 ).
).
6÷(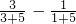 -
-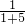 ),
),
=6÷ ,
,
=144(页).
答:这本书有144页.
(2)以全班总人数为单位“1”,开始时达标人数占 ,后来占
,后来占 ,两人对应的分率是(
,两人对应的分率是( -
- ).
).
2÷( -
- ),
),
=2÷ ,
,
=40(人).
答:全班有40人.
分析:(1)此题综合考查同学们对分率和比的理解,学会选择单位“1”.在完成此类题目时,若还是对单位“1”的理解,容易错解,误认为(1)中以未读页数为单位“1”,故“6页”与“( -
- )-
)- ”对应;
”对应;
(2)中未达标人数为单位“1”,“2人”与 -
- 对应.实际上,这两个单位“1”是不同的,如“2”中未达标人数前后已发生变化,并不是同一个量.所以解答此题的关键是要在题中寻找一个不同的量来作单位“1”.
对应.实际上,这两个单位“1”是不同的,如“2”中未达标人数前后已发生变化,并不是同一个量.所以解答此题的关键是要在题中寻找一个不同的量来作单位“1”.
点评:(1)此题解答关键是把比转化为分数,求出6页所对应的分数,用除法列式求出单位“1”.
(2)明确这一过程中总人数未变,根据前后达标人数占总人数分率的变化求出2人占总人数的分率是完成本题的关键.
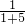 ,两天后是
,两天后是 ,第二天读的页数是(
,第二天读的页数是(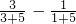 ).
).6÷(
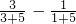 -
-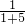 ),
),=6÷
 ,
,=144(页).
答:这本书有144页.
(2)以全班总人数为单位“1”,开始时达标人数占
 ,后来占
,后来占 ,两人对应的分率是(
,两人对应的分率是( -
- ).
).2÷(
 -
- ),
),=2÷
 ,
,=40(人).
答:全班有40人.
分析:(1)此题综合考查同学们对分率和比的理解,学会选择单位“1”.在完成此类题目时,若还是对单位“1”的理解,容易错解,误认为(1)中以未读页数为单位“1”,故“6页”与“(
 -
- )-
)- ”对应;
”对应;(2)中未达标人数为单位“1”,“2人”与
 -
- 对应.实际上,这两个单位“1”是不同的,如“2”中未达标人数前后已发生变化,并不是同一个量.所以解答此题的关键是要在题中寻找一个不同的量来作单位“1”.
对应.实际上,这两个单位“1”是不同的,如“2”中未达标人数前后已发生变化,并不是同一个量.所以解答此题的关键是要在题中寻找一个不同的量来作单位“1”.点评:(1)此题解答关键是把比转化为分数,求出6页所对应的分数,用除法列式求出单位“1”.
(2)明确这一过程中总人数未变,根据前后达标人数占总人数分率的变化求出2人占总人数的分率是完成本题的关键.

练习册系列答案
相关题目